We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Guías de estudio > Intermediate Algebra

Quadratic Equations

12.1 Learning Objectives

  • Recognize a quadratic equation
    • Use the zero product principle to solve quadratic equations that can be factored
    • Identify solutions to quadratic equations on a graph
  • Square Roots and Completing the Square
    • Use the square root property to solve a quadratic equation
    • Complete the square to solve a quadratic equation
  • The Quadratic Formula
    • Write a quadratic equation in standard form and identify the values of a, b, and c in a standard form quadratic equation.
    • Use the Quadratic Formula to find all real solutions of a quadratic equation, recognize when there are no real solutions
    • Solve application problems involving quadratic equations
  • Given a quadratic function in general form, find the vertex of the parabola.
An equation containing a second-degree polynomial is called a quadratic equation. For example, equations such as [latex]2{x}^{2}+3x - 1=0[/latex] and [latex]{x}^{2}-4=0[/latex] are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics. Often the easiest method of solving a quadratic equation is by factoring. Factoring means finding expressions that can be multiplied together to give the expression on one side of the equation. Note that we will not spend a lot of time explaining how to factor in this section.  You may want to seek help if you don't feel confident about factoring. Solving by factoring depends on the zero-product property, which states that if [latex]a\cdot b=0[/latex], then [latex]a=0[/latex] or [latex]b=0[/latex], where a and b are real numbers or algebraic expressions. The process of factoring a quadratic equation depends on the leading coefficient, whether it is 1 or another integer. We will look at both situations; but first, we want to confirm that the equation is written in standard form, [latex]a{x}^{2}+bx+c=0[/latex], where a, b, and c are real numbers, and [latex]a\ne 0[/latex]. The equation [latex]{x}^{2}+x - 6=0[/latex] is in standard form. We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF), and for equations that have special factoring formulas as well, such as the difference of squares, both of which we will see later in this section.

The Zero-Product Property and Quadratic Equations

The zero-product property states
[latex]\text{If }a\cdot b=0,\text{ then }a=0\text{ or }b=0[/latex],
where a and b are real numbers or algebraic expressions. A quadratic equation is an equation containing a second-degree polynomial; for example
[latex]a{x}^{2}+bx+c=0[/latex]
where a, b, and c are real numbers, and if [latex]a\ne 0[/latex], it is in standard form.

12.1.1 Solving Quadratics with a Leading Coefficient of 1

In the quadratic equation [latex]{x}^{2}+x - 6=0[/latex], the leading coefficient, or the coefficient of [latex]{x}^{2}[/latex], is 1. We have one method of factoring quadratic equations in this form.

Reminder: Given a quadratic equation with the leading coefficient of 1, factor it.

  1. Find two numbers whose product equals c and whose sum equals b.
  2. Use those numbers to write two factors of the form [latex]\left(x+k\right)\text{ or }\left(x-k\right)[/latex], where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and [latex]-2[/latex], the factors are [latex]\left(x+1\right)\left(x - 2\right)[/latex].
  3. Solve using the zero-product property by setting each factor equal to zero and solving for the variable.

Example 12.1.a

Factor and solve the equation: [latex]{x}^{2}+x - 6=0[/latex].

Answer: To factor [latex]{x}^{2}+x - 6=0[/latex], we look for two numbers whose product equals [latex]-6[/latex] and whose sum equals 1. Begin by looking at the possible factors of [latex]-6[/latex].

[latex]\begin{array}{l}1\cdot \left(-6\right)\hfill \\ \left(-6\right)\cdot 1\hfill \\ 2\cdot \left(-3\right)\hfill \\ 3\cdot \left(-2\right)\hfill \end{array}[/latex]
The last pair, [latex]3\cdot \left(-2\right)[/latex] sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.
[latex]\left(x - 2\right)\left(x+3\right)=0[/latex]
To solve this equation, we use the zero-product property. Set each factor equal to zero and solve.
[latex]\begin{array}{l}\left(x - 2\right)\left(x+3\right)\hfill&=0\hfill \\ \left(x - 2\right)\hfill&=0\hfill \\ x\hfill&=2\hfill \\ \left(x+3\right)\hfill&=0\hfill \\ x\hfill&=-3\hfill \end{array}[/latex]
The two solutions are [latex]x=2[/latex] and [latex]x=-3[/latex]. If we graph the function [latex]f(x)={x}^{2}+x - 6[/latex], we will get the parabola in the figure below. The solutions to the equation[latex]{x}^{2}+x - 6=0[/latex] are the x-intercepts of the function [latex]f(x)={x}^{2}+x - 6[/latex]. Recall that x-intercepts are where the outputs, or y values are zero, therefore the points (-3,0) and (2,0) represent the places where the parabola crosses the x axis. 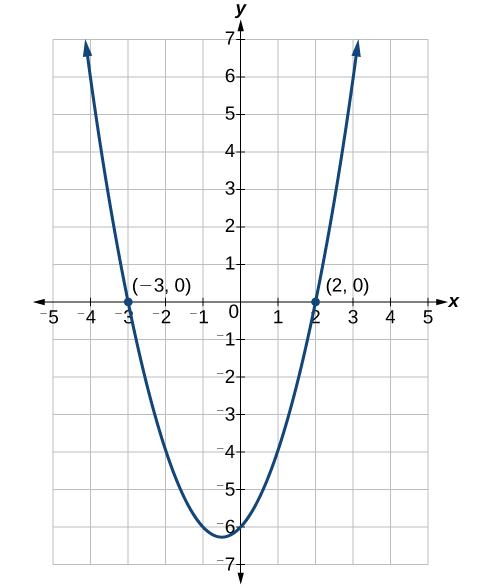Coordinate plane with the x-axis ranging from negative 5 to 5 and the y-axis ranging from negative 7 to 7. The function x squared plus x minus six equals zero is graphed, with the x-intercepts (-3,0) and (2,0), plotted as well.

In the following video we provide more examples of factoring to solve quadratic equations. https://youtu.be/bi7i_RuIGl0   In our next example, we will solve a quadratic equation that is written as a difference of squares.

Example 12.1.b

Solve the difference of squares equation using the zero-product property: [latex]{x}^{2}-9=0[/latex].

Answer: Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property.

[latex]\begin{array}{l}{x}^{2}-9=0\hfill \\ \left(x - 3\right)\left(x+3\right)=0\hfill \\ \hfill \\ \left(x - 3\right)=0\hfill \\ x=3\hfill \\ \hfill \\ \left(x+3\right)=0\hfill \\ x=-3\hfill \end{array}[/latex]
The solutions are [latex]x=3[/latex] and [latex]x=-3[/latex].

 12.1.2 Solving Quadratics with a Leading Coefficient of [latex]\ne1[/latex]

Recall that when the leading coefficient is not 1, we factor a quadratic equation using the method called grouping, which requires four terms. With the equation in standard form, let’s review the grouping procedures:
  1. With the quadratic in standard form, [latex]a{x}^{2}+bx+c=0[/latex], multiply [latex]a\cdot c[/latex].
  2. Find two numbers whose product equals [latex]ac[/latex] and whose sum equals [latex]b[/latex].
  3. Rewrite the equation replacing the [latex]bx[/latex] term with two terms using the numbers found in step 1 as coefficients of x.
  4. Factor the first two terms and then factor the last two terms. The expressions in parentheses must be exactly the same to use grouping.
  5. Factor out the expression in parentheses.
  6. Set the expressions equal to zero and solve for the variable.

Example 12.1.c

Use grouping to factor and solve the quadratic equation: [latex]4{x}^{2}+15x+9=0[/latex].

Answer: First, multiply [latex]ac:4\left(9\right)=36[/latex]. Then list the factors of [latex]36[/latex].

[latex]\begin{array}{l}1\cdot 36\hfill \\ 2\cdot 18\hfill \\ 3\cdot 12\hfill \\ 4\cdot 9\hfill \\ 6\cdot 6\hfill \end{array}[/latex]
The only pair of factors that sums to [latex]15[/latex] is [latex]3+12[/latex]. Rewrite the equation replacing the b term, [latex]15x[/latex], with two terms using 3 and 12 as coefficients of x. Factor the first two terms, and then factor the last two terms.
[latex]\begin{array}{l}4{x}^{2}+3x+12x+9=0\hfill \\ x\left(4x+3\right)+3\left(4x+3\right)=0\hfill \\ \left(4x+3\right)\left(x+3\right)=0\hfill \end{array}[/latex]
Solve using the zero-product property.
[latex]\begin{array}{l}\left(4x+3\right)\left(x+3\right)=0\hfill \\ \hfill \\ \left(4x+3\right)=0\hfill \\ x=-\frac{3}{4}\hfill \\ \hfill \\ \left(x+3\right)=0\hfill \\ x=-3\hfill \end{array}[/latex]
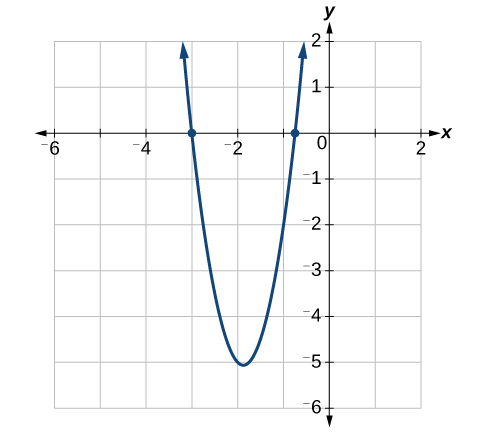
The solutions are [latex]x=-\frac{3}{4}[/latex], [latex]x=-3[/latex]. Coordinate plane with the x-axis ranging from negative 6 to 2 with every other tick mark labeled and the y-axis ranging from negative 6 to 2 with each tick mark numbered. The equation: four x squared plus fifteen x plus nine is graphed with its x-intercepts: (-3/4,0) and (-3,0) plotted as well.

The following video contains another example of solving a quadratic equation using factoring with grouping. https://youtu.be/04zEXaOiO4U Sometimes, we may be given an equation that does not look like a quadratic at first glance. In our next examples we will solve a cubic polynomial equation where the GCF of each term is x, and can be factored.  The result is a quadratic equation that we can solve.

Example 12.1.d

Solve the equation by factoring: [latex]-3{x}^{3}-5{x}^{2}-2x=0[/latex].

Answer: This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out [latex]-x[/latex] from all of the terms and then proceed with grouping.

[latex]\begin{array}{l}-3{x}^{3}-5{x}^{2}-2x=0\hfill \\ -x\left(3{x}^{2}+5x+2\right)=0\hfill \end{array}[/latex]
Use grouping on the expression in parentheses.
[latex]\begin{array}{l}-x\left(3{x}^{2}+3x+2x+2\right)=\hfill&0\hfill \\ -x\left[3x\left(x+1\right)+2\left(x+1\right)\right]=\hfill&0\hfill \\ -x\left(3x+2\right)\left(x+1\right)=\hfill&0\hfill \end{array}[/latex]
Now, we use the zero-product property. Notice that we have three factors.
[latex]\begin{array}{l}-x\hfill&=0\hfill \\ x\hfill&=0\hfill \\ 3x+2\hfill&=0\hfill \\ x\hfill&=-\frac{2}{3}\hfill \\ x+1\hfill&=0\hfill \\ x\hfill&=-1\hfill \end{array}[/latex]
The solutions are [latex]x=0[/latex], [latex]x=-\frac{2}{3}[/latex], and [latex]x=-1[/latex].

  In this last video example, we solve a quadratic equation with a leading coefficient of -1 using a shortcut method of factoring and the zero product principle. https://youtu.be/nZYfgHygXis Quadratic equations can be solved in many ways. You may already be familiar with factoring to solve some quadratic equations. However, not all quadratic equations can be factored. In this topic, you will use square roots to learn another way to solve quadratic equations—and this method will work with all quadratic equations.

12.1.3 Solve a Quadratic Equation by the Square Root Property

One way to solve the quadratic equation [latex]x^{2}=9[/latex] is to subtract 9 from both sides to get one side equal to 0: [latex]x^{2}-9=0[/latex]. The expression on the left can be factored, it is a difference of squares: [latex]\left(x+3\right)\left(x–3\right)=0[/latex]. Using the zero factor property, you know this means [latex]x+3=0[/latex] or [latex]x–3=0[/latex], so [latex]x=−3[/latex] or 3. Another property would let you solve that equation more easily is called the square root property.

The Square Root Property

If [latex]x^{2}=a[/latex], then [latex] x=\sqrt{a}[/latex] or [latex] -\sqrt{a}[/latex]. The property above says that you can take the square root of both sides of an equation, but you have to think about two cases: the positive square root of a and the negative square root of a.
A shortcut way to write “[latex] \sqrt{a}[/latex]” or “[latex] -\sqrt{a}[/latex]” is [latex] \pm \sqrt{a}[/latex]. The symbol [latex]\pm[/latex] is often read “positive or negative.” If it is used as an operation (addition or subtraction), it is read “plus or minus.”

Example 12.1.e

Solve using the Square Root Property. [latex]x^{2}=9[/latex]

Answer: Since one side is simply [latex]x^{2}[/latex], you can take the square root of both sides to get x on one side. Don’t forget to use both positive and negative square roots!

[latex]\begin{array}{l}x^{2}=9\\\,\,\,x=\pm\sqrt{9}\\\,\,\,x=\pm3\end{array}[/latex]

Answer

[latex]x=\pm3[/latex] (that is, [latex]x=3[/latex] or [latex]-3[/latex])

Notice that there is a difference here in solving [latex]x^{2}=9[/latex] and finding [latex] \sqrt{9}[/latex]. For [latex]x^{2}=9[/latex], you are looking for all numbers whose square is 9. For [latex] \sqrt{9}[/latex], you only want the principal (nonnegative) square root. The negative of the principal square root is [latex] -\sqrt{9}[/latex]; both would be [latex] \pm \sqrt{9}[/latex]. Unless there is a symbol in front of the radical sign, only the nonnegative value is wanted! In the example above, you can take the square root of both sides easily because there is only one term on each side. In some equations, you may need to do some work to get the equation in this form. You will find that this involves isolating [latex]x^{2}[/latex]. In our first video we will show more examples of using the square root property to solve a quadratic equation. https://youtu.be/Fj-BP7uaWrI

Example 12.1.f

Solve. [latex]10x^{2}+5=85[/latex]

Answer: If you try taking the square root of both sides of the original equation, you will have [latex] \sqrt{10{{x}^{2}}+5}[/latex] on the left, and you can’t simplify that. Subtract 5 from both sides to get the [latex]x^{2}[/latex] term by itself.

[latex]10x^{2}+5=85[/latex]

You could now take the square root of both sides, but you would have [latex] \sqrt{10}[/latex] as a coefficient, and you would need to divide by that coefficient. Dividing by 10 before you take the square root will be a little easier.

[latex]10x^{2}=80[/latex]

Now you have only [latex]x^{2}[/latex] on the left, so you can use the Square Root Property easily. Be sure to simplify the radical if possible.

[latex] \begin{array}{l}{{x}^{2}}=8\\\,\,\,x=\pm \sqrt{8}\\\,\,\,\,\,\,=\pm \sqrt{(4)(2)}\\\,\,\,\,\,\,=\pm \sqrt{4}\sqrt{2}\\\,\,\,\,\,\,=\pm 2\sqrt{2}\end{array}[/latex]

Answer

[latex-display] x=\pm 2\sqrt{2}[/latex-display]

Sometimes more than just the x is being squared:

Example 12.1.g

Solve. [latex]\left(x–2\right)^{2}–50=0[/latex]

Answer: Again, taking the square root of both sides at this stage will leave something you can’t work with on the left. Start by adding 50 to both sides.

[latex]\left(x-2\right)^{2}-50=0[/latex]

Because [latex]\left(x–2\right)^{2}[/latex] is a squared quantity, you can take the square root of both sides.

[latex]\begin{array}{r}\left(x-2\right)^{2}=50\,\,\,\,\,\,\,\,\,\,\\x-2=\pm\sqrt{50}\end{array}[/latex]

To isolate x on the left, you need to add 2 to both sides. Be sure to simplify the radical if possible.

[latex] \begin{array}{l}x=2\pm \sqrt{50}\\\,\,\,\,=2\pm \sqrt{(25)(2)}\\\,\,\,\,=2\pm \sqrt{25}\sqrt{2}\\\,\,\,\,=2\pm 5\sqrt{2}\end{array}[/latex]

Answer

[latex-display] x=2\pm 5\sqrt{2}[/latex-display]

In the next video you will see more examples of using square roots to solve quadratic equations. https://youtu.be/4H5qZ_-8YM4

12.1.4 Solve a Quadratic Equation by Completing the Square

Not all quadratic equations can be factored or solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square. Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property. First, let's make sure we can recognize a perfect square trinomial and how factor it.

Example 12.1.h

Factor [latex]9x^{2}–24x+16[/latex].

Answer: First notice that the [latex]x^{2}[/latex] term and the constant term are both perfect squares. [latex-display]\begin{array}{l}9x^{2}=\left(3x\right)^{2}\\\,\,\,16=4^{2}\end{array}[/latex-display] Then notice that the middle term (ignoring the sign) is twice the product of the square roots of the other terms. [latex-display]24x=2\left(3x\right)\left(4\right)[/latex-display] A trinomial in the form [latex]r^{2}-2rs+s^{2}[/latex] can be factored as [latex](r–s)^{2}[/latex]. In this case, the middle term is subtracted, so subtract r and s and square it to get [latex](r–s)^{2}[/latex]. [latex-display]\begin{array}{c}\,\,\,r=3x\\s=4\\9x^{2}-24x+16=\left(3x-4\right)^{2}\end{array}[/latex-display]

If this were an equation, we could solve using either the square root property or the zero product property. If you don't start with a perfect square trinomial, you can complete the square to make what you have into one. To complete the square, the leading coefficient, a, must equal 1. If it does not, then divide the entire equation by a. Then, we can use the following procedures to solve a quadratic equation by completing the square.

Steps for Completing The Square

We will use the example [latex]{x}^{2}+4x+1=0[/latex] to illustrate each step.
  1. Given a quadratic equation that cannot be factored, and with [latex]a=1[/latex], first add or subtract the constant term to the right side of the equal sign.
    [latex]{x}^{2}+4x=-1[/latex]
  2. Multiply the b term by [latex]\frac{1}{2}[/latex] and square it.
    [latex]\begin{array}{l}\frac{1}{2}\left(4\right)=2\hfill \\ {2}^{2}=4\hfill \end{array}[/latex]
  3. Add [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex] to both sides of the equal sign and simplify the right side. We have
    [latex]\begin{array}{l}{x}^{2}+4x+4=-1+4\hfill \\ {x}^{2}+4x+4=3\hfill \end{array}[/latex]
  4. The left side of the equation can now be factored as a perfect square.
    [latex]\begin{array}{l}{x}^{2}+4x+4=3\hfill \\ {\left(x+2\right)}^{2}=3\hfill \end{array}[/latex]
  5. Use the square root property and solve.
    [latex]\begin{array}{l}\sqrt{{\left(x+2\right)}^{2}}=\pm \sqrt{3}\hfill \\ x+2=\pm \sqrt{3}\hfill \\ x=-2\pm \sqrt{3}\hfill \end{array}[/latex]
  6. The solutions are [latex]x=-2+\sqrt{3}[/latex], [latex]x=-2-\sqrt{3}[/latex].

Example 12.1.i

Solve by completing the square. [latex]x^{2}–12x–4=0[/latex]

Answer: Since you cannot factor the trinomial on the left side, you will use completing the square to solve the equation. First, move the constant term to the right side of the equal sign.Identify b.

[latex]\begin{array}{r}x^{2}-12x=4\,\,\,\,\,\,\,\,\\b=-12\end{array}[/latex]

Then, take [latex]\frac{1}{2}[/latex] of the b term and square it. Add [latex] {{\left( \frac{b}{2}\right)}^{2}}[/latex] to complete the square, so [latex] {{\left( \frac{b}{2} \right)}^{2}}={{\left( \frac{-12}{2} \right)}^{2}}={{\left( -6 \right)}^{2}}=36[/latex]. Add the value to both sides of the equation and simplify.

[latex]\begin{array}{l}x^{2}-12x+36=4+36\\x^{2}-12x+36=40\end{array}[/latex]

Rewrite the left side as a squared binomial.

[latex]\left(x-6\right)^{2}=40[/latex]

Use the Square Root Property. Remember to include both the positive and negative square root, or you’ll miss one of the solutions.

[latex] x-6=\pm\sqrt{40}[/latex]

Solve for x by adding 6 to both sides. Simplify as needed.

[latex] \begin{array}{l}x=6\pm \sqrt{40}\\\,\,\,\,=6\pm \sqrt{4}\sqrt{10}\\\,\,\,\,=6\pm 2\sqrt{10}\end{array}[/latex]

Answer

[latex-display] x=6\pm 2\sqrt{10}[/latex-display]

Example 12.1.j

Solve by completing the square: [latex]{x}^{2}-3x - 5=0[/latex].

Answer: First, move the constant term to the right side of the equal sign.

[latex]{x}^{2}-3x=5[/latex]
Identify b.[latex]b=-3[/latex] Then, take [latex]\frac{1}{2}[/latex] of the b term and square it.
[latex]\begin{array}{l}\frac{1}{2}\left(-3\right)=-\frac{3}{2}\hfill \\ {\left(-\frac{3}{2}\right)}^{2}=\frac{9}{4}\hfill \end{array}[/latex]
Add the result to both sides of the equal sign.
[latex]\begin{array}{l}\text{ }{x}^{2}-3x+{\left(-\frac{3}{2}\right)}^{2}=5+{\left(-\frac{3}{2}\right)}^{2}\hfill \\ {x}^{2}-3x+\frac{9}{4}=5+\frac{9}{4}\hfill \end{array}[/latex]
Factor the left side as a perfect square and simplify the right side.
[latex]{\left(x-\frac{3}{2}\right)}^{2}=\frac{29}{4}[/latex]
Use the square root property and solve.
[latex]\begin{array}{l}\sqrt{{\left(x-\frac{3}{2}\right)}^{2}}\hfill&=\pm \sqrt{\frac{29}{4}}\hfill \\ \left(x-\frac{3}{2}\right)\hfill&=\pm \frac{\sqrt{29}}{2}\hfill \\ x\hfill&=\frac{3}{2}\pm \frac{\sqrt{29}}{2}\hfill \end{array}[/latex]
The solutions are [latex]x=\frac{3}{2}+\frac{\sqrt{29}}{2}[/latex], [latex]x=\frac{3}{2}-\frac{\sqrt{29}}{2}[/latex].

In the next video you will see more examples of how to use completing the square to solve a quadratic equation. https://youtu.be/PsbYUySRjFo You may have noticed that because you have to use both square roots, all the examples have two solutions. Here is another example that’s slightly different.

Example 12.1.k

Solve by completing the square. [latex]x^{2}+16x+17=-47[/latex].

Answer: Rewrite the equation so the left side has the form [latex]x^{2}+bx[/latex]. Identify b.

[latex]\begin{array}{c}x^{2}+16x=-64\\b=16\end{array}[/latex]

Add [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex], which is [latex] {{\left( \frac{16}{2} \right)}^{2}}={{8}^{2}}=64[/latex], to both sides.

[latex]\begin{array}{l}x^{2}+16x+64=-64+64\\x^{2}+16x+64=0\end{array}[/latex]

Write the left side as a squared binomial.

[latex]\left(x+8\right)^{2}=0[/latex]

Take the square roots of both sides. Normally both positive and negative square roots are needed, but 0 is neither positive nor negative. 0 has only one root.

[latex]x+8=0[/latex]

Solve for x.

[latex]x=-8[/latex]

Answer

[latex-display]x=-8[/latex-display]

Take a closer look at this problem and you may see something familiar. Instead of completing the square, try adding 47 to both sides in the equation. The equation [latex]x^{2}+16x+17=−47[/latex] becomes [latex]x^{2}+16x+64=0[/latex]. Can you factor this equation using grouping? (Think of two numbers whose product is 64 and whose sum is 16). It can be factored as [latex](x+8)(x+8)=0[/latex], of course! Knowing how to complete the square is very helpful, but it is not always the only way to solve an equation. In our last video, we show an example of how to use completing the square to solve a quadratic equation whose solutions are rational. https://youtu.be/IjCjbtrPWHM

12.1.5 The Quadratic Formula

You can solve any quadratic equation by completing the square—rewriting part of the equation as a perfect square trinomial. If you complete the square on the generic equation [latex]ax^{2}+bx+c=0[/latex] and then solve for x, you find that [latex]x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex]. This equation is known as the Quadratic Formula. We can derive the quadratic formula by completing the square. First, assume that the leading coefficient is positive; if it is negative, we can multiply the equation by [latex]-1[/latex] and obtain a positive a. Given [latex]a{x}^{2}+bx+c=0[/latex], [latex]a\ne 0[/latex], we will complete the square as follows:
  1. First, move the constant term to the right side of the equal sign:
    [latex]a{x}^{2}+bx=-c[/latex]
  2. As we want the leading coefficient to equal 1, divide through by a:
    [latex]{x}^{2}+\frac{b}{a}x=-\frac{c}{a}[/latex]
  3. Then, find [latex]\frac{1}{2}[/latex] of the middle term, and add [latex]{\left(\frac{1}{2}\frac{b}{a}\right)}^{2}=\frac{{b}^{2}}{4{a}^{2}}[/latex] to both sides of the equal sign:
    [latex]{x}^{2}+\frac{b}{a}x+\frac{{b}^{2}}{4{a}^{2}}=\frac{{b}^{2}}{4{a}^{2}}-\frac{c}{a}[/latex]
  4. Next, write the left side as a perfect square. Find the common denominator of the right side and write it as a single fraction:
    [latex]{\left(x+\frac{b}{2a}\right)}^{2}=\frac{{b}^{2}-4ac}{4{a}^{2}}[/latex]
  5. Now, use the square root property, which gives
    [latex]\begin{array}{l}x+\frac{b}{2a}=\pm \sqrt{\frac{{b}^{2}-4ac}{4{a}^{2}}}\hfill \\ x+\frac{b}{2a}=\frac{\pm \sqrt{{b}^{2}-4ac}}{2a}\hfill \end{array}[/latex]
  6. Finally, add [latex]-\frac{b}{2a}[/latex] to both sides of the equation and combine the terms on the right side. Thus,
    [latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex]
This formula is very helpful for solving quadratic equations that are difficult or impossible to factor, and using it can be faster than completing the square. The Quadratic Formula can be used to solve any quadratic equation of the form [latex]ax^{2}+bx+c=0[/latex]. The form [latex]ax^{2}+bx+c=0[/latex] is called standard form of a quadratic equation. Before solving a quadratic equation using the Quadratic Formula, it's vital that you be sure the equation is in this form. If you don't, you might use the wrong values for a, b, or c, and then the formula will give incorrect solutions.

12.1.6 Solving a Quadratic Equation using the Quadratic Formula

The Quadratic Formula will work with any quadratic equation, but only if the equation is in standard form, [latex]ax^{2}+bx+c=0[/latex]. To use it, follow these steps.
  • Put the equation in standard form first.
  • Identify the coefficients, a, b, and c. Be careful to include negative signs if the bx or c terms are subtracted.
  • Carefully substitute the values noted in step 2 into the equation. To avoid needless errors, use parentheses around each number input into the formula.
  • Simplify as much as possible.
  • Use the [latex]\pm[/latex] in front of the radical to separate the solution into two values: one in which the square root is added, and one in which it is subtracted.
  • Simplify both values to get the possible solutions.
That's a lot of steps. Let’s try using the Quadratic Formula to solve a relatively simple equation first; then you’ll go back and solve it again using another factoring method.

Example 12.1.l

Use the Quadratic Formula to solve the equation [latex]x^{2}+4x=5[/latex].

Answer: First write the equation in standard form.

[latex]\begin{array}{r}x^{2}+4x=5\,\,\,\\x^{2}+4x-5=0\,\,\,\\\\a=1,b=4,c=-5\end{array}[/latex]

Note that the subtraction sign means the constant c is negative.

[latex] \begin{array}{r}{{x}^{2}}\,\,\,+\,\,\,4x\,\,\,-\,\,\,5\,\,\,=\,\,\,0\\\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\a{{x}^{2}}\,\,\,+\,\,\,bx\,\,\,+\,\,\,c\,\,\,=\,\,\,0\end{array}[/latex]

Substitute the values into the Quadratic Formula. [latex] x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\[/latex]

[latex] \begin{array}{l}\\x=\frac{-4\pm \sqrt{{{(4)}^{2}}-4(1)(-5)}}{2(1)}\end{array}[/latex]

Simplify, being careful to get the signs correct.

[latex]x=\frac{-4\pm\sqrt{16+20}}{2}[/latex]

Simplify some more.

[latex] x=\frac{-4\pm \sqrt{36}}{2}[/latex]

Simplify the radical: [latex] \sqrt{36}=6[/latex].

[latex] x=\frac{-4\pm 6}{2}[/latex]

Separate and simplify to find the solutions to the quadratic equation. Note that in one, 6 is added and in the other, 6 is subtracted.

[latex]\begin{array}{c}x=\frac{-4+6}{2}=\frac{2}{2}=1\\\\\text{or}\\\\x=\frac{-4-6}{2}=\frac{-10}{2}=-5\end{array}[/latex]

Answer

[latex-display]x=1\,\,\,\text{or}\,\,\,-5[/latex-display]

You can check these solutions by substituting [latex]1[/latex] and [latex]−5[/latex] into the original equation.
[latex]\begin{array}{r}x=1\\x^{2}+4x=5\\\left(1\right)^{2}+4\left(1\right)=5\\1+4=5\\5=5\end{array}[/latex] [latex]\begin{array}{r}x=-5\\x^{2}+4x=5\,\,\,\,\,\\\left(-5\right)^{2}+4\left(-5\right)=5\,\,\,\,\,\\25-20=5\,\,\,\,\,\\5=5\,\,\,\,\,\end{array}[/latex]
You get two true statements, so you know that both solutions work: [latex]x=1[/latex] or [latex]-5[/latex]. You’ve solved the equation successfully using the Quadratic Formula! Watch this video to see an example of how to use the quadratic formula to solve a quadratic equation that has two real, rational solutions. https://youtu.be/xtwO-n8lRPw Sometimes, it may be easier to solve an equation using conventional factoring methods, like finding number pairs that sum to one number (in this example, 4) and that produce a specific product (in this example [latex]−5[/latex]) when multiplied. The power of the Quadratic Formula is that it can be used to solve any quadratic equation, even those where finding number combinations will not work. In the next video example we show that the quadratic formula is useful when a quadratic equation has two irrational solutions that could not have been obtained by factoring. https://youtu.be/tF0muV86dr0 Most of the quadratic equations you've looked at have two solutions, like the one above. The following example is a little different.

Example 12.1.m

Use the Quadratic Formula to solve the equation [latex]x^{2}-2x=6x-16[/latex].

Answer: Subtract 6x from each side and add 16 to both sides to put the equation in standard form.

[latex]\begin{array}{l}x^{2}-2x=6x-16\\x^{2}-2x-6x+16=0\\x^{2}-8x+16=0\end{array}[/latex]

Identify the coefficients a, b, and c. [latex]x^{2}=1x^{2}[/latex], so [latex]a=1[/latex]. Since [latex]8x[/latex] is subtracted, b is negative. [latex]a=1,b=-8,c=16[/latex]

[latex] \begin{array}{r}{{x}^{2}}\,\,\,-\,\,\,8x\,\,\,+\,\,\,16\,\,\,=\,\,\,0\\\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\a{{x}^{2}}\,\,\,+\,\,\,bx\,\,\,+\,\,\,\,c\,\,\,\,=\,\,\,0\end{array}[/latex]

Substitute the values into the Quadratic Formula.

[latex]\begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-(-8)\pm \sqrt{{{(-8)}^{2}}-4(1)(16)}}{2(1)}\end{array}[/latex]

Simplify.

[latex] x=\frac{8\pm \sqrt{64-64}}{2}[/latex]

Since the square root of 0 is 0, and both adding and subtracting 0 give the same result, there is only one possible value.

[latex] x=\frac{8\pm \sqrt{0}}{2}=\frac{8}{2}=4[/latex]

Answer

[latex-display]x=4[/latex-display]

Again, check using the original equation.

[latex]\begin{array}{r}x^{2}-2x=6x-16\,\,\,\,\,\\\left(4\right)^{2}-2\left(4\right)=6\left(4\right)-16\\16-8=24-16\,\,\,\,\,\,\\8=8\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

In the next example, we will show that some quadratic equations do not have real solutions.  As we simplify with the quadratic formula, we may end up with a negative number under a square root, which, as we know, is not defined for real numbers.

Example 12.1.n

Use the Quadratic Formula to solve the equation [latex]x^2+x=-x-3[/latex]

Answer: Add x to both sides, and add 3 to both sides to get the quadratic equation in standard form.

[latex]\begin{array}{l}x^{2}+x=-x-3\\x^{2}+2x+3=0\end{array}[/latex]

Identify a, b, c.

[latex]a=1, b=2, c=3[/latex]

Substitute values for a, b, c into the quadratic formula.

[latex]\begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-2\pm \sqrt{{{(2)}^{2}}-4(1)(3)}}{2(1)}\end{array}[/latex]

Simplify

[latex] x=\frac{-2\pm \sqrt{-8}}{2}[/latex]

Since the square root of a negative number is not defined for real numbers, there are no real number solutions to this equation.

 Answer

There are no real solutions.

12.1.7 Given a quadratic function in general form, find the vertex of the parabola.

One reason we may want to identify the vertex of the parabola is that this point will inform us where the maximum or minimum value of the output occurs, (k), and where it occurs, (x). If we are given the general form of a quadratic function:

[latex]f(x)=ax^2+bx+c[/latex]

We can define the vertex, [latex](h,k)[/latex], by doing the following:
  • Identify a, b, and c.
  • Find h, the x-coordinate of the vertex, by substituting a and b into [latex]h=-\frac{b}{2a}[/latex].
  • Find k, the y-coordinate of the vertex, by evaluating [latex]k=f\left(h\right)=f\left(-\frac{b}{2a}\right)[/latex]

Example: Finding the Vertex of a Quadratic Function

Find the vertex of the quadratic function [latex]f\left(x\right)=2{x}^{2}-6x+7[/latex]. Rewrite the quadratic in standard form (vertex form).

Answer: The horizontal coordinate of the vertex will be at

[latex]\begin{array}{c}h=-\frac{b}{2a}\hfill \\ \text{ }=-\frac{-6}{2\left(2\right)}\hfill \\ \text{ }=\frac{6}{4}\hfill \\ \text{ }=\frac{3}{2}\hfill \end{array}[/latex]

The vertical coordinate of the vertex will be at

[latex]\begin{array}{c}k=f\left(h\right)\hfill \\ \text{ }=f\left(\frac{3}{2}\right)\hfill \\ \text{ }=2{\left(\frac{3}{2}\right)}^{2}-6\left(\frac{3}{2}\right)+7\hfill \\ \text{ }=\frac{5}{2}\hfill \end{array}[/latex]

Rewriting into standard form, the stretch factor will be the same as the [latex]a[/latex] in the original quadratic.

[latex]\begin{array}{c}f\left(x\right)=a{x}^{2}+bx+c\hfill \\ f\left(x\right)=2{x}^{2}-6x+7\hfill \end{array}[/latex]

Using the vertex to determine the shifts,

[latex]f\left(x\right)=2{\left(x-\frac{3}{2}\right)}^{2}+\frac{5}{2}[/latex]

12.1.8 Applying the Quadratic Formula

Quadratic equations are widely used in science, business, and engineering. Quadratic equations are commonly used in situations where two things are multiplied together and they both depend on the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, you use a quadratic equation. Because the quantity of a product sold often depends on the price, you sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge. A very common and easy-to-understand application is the height of a ball thrown at the ground off a building. Because gravity will make the ball speed up as it falls, a quadratic equation can be used to estimate its height any time before it hits the ground. Note: The equation isn't completely accurate, because friction from the air will slow the ball down a little. For our purposes, this is close enough.

Example 12.1.o

A ball is thrown off a building from 200 feet above the ground. Its starting velocity (also called initial velocity) is [latex]−10[/latex] feet per second. (The negative value means it's heading toward the ground.) The equation [latex]h=-16t^{2}-10t+200[/latex] can be used to model the height of the ball after t seconds. About how long does it take for the ball to hit the ground?

Answer: When the ball hits the ground, the height is 0. Substitute 0 for h.

[latex]\begin{array}{c}h=-16t^{2}-10t+200\\0=-16t^{2}-10t+200\\-16t^{2}-10t+200=0\end{array}[/latex]

This equation is difficult to solve by factoring or by completing the square, so solve it by applying the Quadratic Formula, [latex] x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex]. In this case, the variable is t rather than x. [latex]a=−16,b=−10[/latex], and [latex]c=200[/latex].

[latex] t=\frac{-(-10)\pm \sqrt{{{(-10)}^{2}}-4(-16)(200)}}{2(-16)}[/latex]

Simplify. Be very careful with the signs.

[latex] \begin{array}{l}t=\frac{10\pm \sqrt{100+12800}}{-32}\\\,\,=\frac{10\pm \sqrt{12900}}{-32}\end{array}[/latex]

Use a calculator to find both roots.

t is approximately [latex]−3.86[/latex] or [latex]3.24[/latex].

Consider the roots logically. One solution, [latex]−3.86[/latex], cannot be the time because it is a negative number. The other solution, [latex]3.24[/latex] seconds, must be when the ball hits the ground.

Answer

The ball hits the ground approximately [latex]3.24[/latex] seconds after being thrown.

In the next video we show another example of how the quadratic equation can be used to find the time it takes for an object in free fall to hit the ground. https://youtu.be/RcVeuJhcuL0
The area problem below does not look like it includes a Quadratic Formula of any type, and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.

Example 12.1.p

Bob made a quilt that is 4 ft [latex]\times[/latex] 5 ft. He has 10 sq. ft. of fabric he can use to add a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.)

Answer: Sketch the problem. Since you don’t know the width of the border, you will let the variable x represent the width. In the diagram, the original quilt is indicated by the red rectangle. The border is the area between the red and blue lines. A blue rectangle. Within the blue rectangle are a pair of vertical parallel lines and a pair of horizontal parallel lines that create a smaller red rectangle. The lengths of this red rectangle are 4 feet and 5 feet. The line segments between the boundaries of the red rectangle and the bigger blue rectangle are all labeled x. Since each side of the original 4 by 5 quilt has the border of width x added, the length of the quilt with the border will be [latex]5+2x[/latex], and the width will be [latex]4+2x[/latex]. (Both dimensions are written in terms of the same variable, and you will multiply them to get an area! This is where you might start to think that a quadratic equation might be used to solve this problem.) A blue rectangle with one side a height of 4+2x and another side a length of 5+2x. Within the blue rectangle are a pair of vertical parallel lines and a pair of horizontal parallel lines that create a smaller red rectangle. The height of this red rectangle is 4 feet and the length is 5 feet. The line segments between the boundaries of the red rectangle and the bigger blue rectangle are all labeled x. You are only interested in the area of the border strips. Write an expression for the area of the border.

Area of border = Area of the blue rectangle minus the area of the red rectangle

Area of border[latex]=\left(4+2x\right)\left(5+2x\right)–\left(4\right)\left(5\right)[/latex]

There are 10 sq ft of fabric for the border, so set the area of border to be 10.

[latex]10=\left(4+2x\right)\left(5+2x\right)–20[/latex]

Multiply [latex]\left(4+2x\right)\left(5+2x\right)[/latex].

[latex]10=20+8x+10x+4x^{2}–20[/latex]

Simplify.

[latex]10=18x+4x^{2}[/latex]

Subtract 10 from both sides so that you have a quadratic equation in standard form and can apply the Quadratic Formula to find the roots of the equation.

[latex]\begin{array}{c}0=18x+4x^{2}-10\\\\\text{or}\\\\4x^{2}-10\\\\2\left(2x^{2}+9x-5\right)=0\end{array}[/latex]

Factor out the greatest common factor, 2, so that you can work with the simpler equivalent equation, [latex]2x^{2}+9x–5=0[/latex].

[latex]\begin{array}{r}2\left(2x^{2}+9x-5\right)=0\\\\\frac{2\left(2x^{2}+9x-5\right)}{2}=\frac{0}{2}\\\\2x^{2}+9x-5=0\end{array}[/latex]

Use the Quadratic Formula. In this case, [latex]a=2,b=9[/latex], and [latex]c=−5[/latex].

[latex]\begin{array}{l}x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\\\\x=\frac{-9\pm \sqrt{{{9}^{2}}-4(2)(-5)}}{2(2)}\end{array}[/latex]

Simplify.

[latex] x=\frac{-9\pm \sqrt{121}}{4}=\frac{-9\pm 11}{4}[/latex]

Find the solutions, making sure that the [latex]\pm[/latex] is evaluated for both values.

[latex]\begin{array}{c}x=\frac{-9+11}{4}=\frac{2}{4}=\frac{1}{2}=0.5\\\\\text{or}\\\\x=\frac{-9-11}{4}=\frac{-20}{4}=-5\end{array}[/latex]

Ignore the solution [latex]x=−5[/latex], since the width could not be negative.

Answer

The width of the border should be 0.5 ft.

Our last video gives another example of using the quadratic formula for a geometry problem involving the border around a quilt. https://youtu.be/Zxe-SdwutxA

Quadratic Formula Summary

Quadratic equations can appear in different applications. The Quadratic Formula is a useful way to solve these equations, or any other quadratic equation! The Quadratic Formula, [latex] x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}[/latex], is found by completing the square of the quadratic equation [latex] [/latex]. When you simplify using the quadratic formula and your result is a negative number under a square root, there are no real number solutions to the equation.

Summary

You can find the solutions, or roots, of quadratic equations by setting one side equal to zero, factoring the polynomial, and then applying the Zero Product Property. The Principle of Zero Products states that if [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are 0. Once the polynomial is factored, set each factor equal to zero and solve them separately. The answers will be the set of solutions for the original equation. Not all solutions are appropriate for some applications. In many real-world situations, negative solutions are not appropriate and must be discarded. Completing the square is used to change a binomial of the form [latex]x^{2}+bx[/latex] into a perfect square trinomial [latex] {{x}^{2}}+bx+{{\left( \frac{b}{2} \right)}^{2}}[/latex], which can be factored to [latex] {{\left( x+\frac{b}{2} \right)}^{2}}[/latex]. When solving quadratic equations by completing the square, be careful to add [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex] to both sides of the equation to maintain equality. The Square Root Property can then be used to solve for x. With the Square Root Property, be careful to include both the principal square root and its opposite. Be sure to simplify as needed.

Licenses & Attributions

CC licensed content, Original

  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Quadratic Formula Application - Time for an Object to Hit the Ground. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Quadratic Formula Application - Determine the Width of a Border. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.
  • Ex: Solve a Quadratic Equation Using Factor By Grouping. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Factor and Solve Quadratic Equation - Trinomial a = -1. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • Ex 1: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex 2: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com) . License: Public Domain: No Known Copyright.
  • Ex 1: Completing the Square - Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) . License: Public Domain: No Known Copyright.
  • Ex 2: Completing the Square - Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex2: Quadratic Formula - Two Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex: Quadratic Formula - Two Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.