Positional Systems and Bases
More important than the form of the number symbols is the development of the place value system. Although it is in slight dispute, the earliest known document in which the Indian system displays a positional system dates back to 346 CE. However, some evidence suggests that they may have actually developed a positional system as far back as the first century CE. In this lesson we will explore positional systems an their historical development. We will also discuss some of the positional systems that have been used throughout history and the bases used for those systems. Finally, we will learn how to convert numbers between bases and systems.Learning Objectives
- Become familiar with the history of positional number systems
- Identify bases that have been used in number systems historically
- Convert numbers between bases
- Use two different methods for converting numbers between bases
The Positional System and Base 10
The Indians were not the first to use a positional system. The Babylonians (as we will see in Chapter 3) used a positional system with 60 as their base. However, there is not much evidence that the Babylonian system had much impact on later numeral systems, except with the Greeks. Also, the Chinese had a base-10 system, probably derived from the use of a counting board.[footnote]Ibid, page 230[/footnote] Some believe that the positional system used in India was derived from the Chinese system. Wherever it may have originated, it appears that around 600 CE, the Indians abandoned the use of symbols for numbers higher than nine and began to use our familiar system where the position of the symbol determines its overall value.[footnote]Ibid, page 231.[/footnote] Numerous documents from the seventh century demonstrate the use of this positional system. Interestingly, the earliest dated inscriptions using the system with a symbol for zero come from Cambodia. In 683, the 605th year of the Saka era is written with three digits and a dot in the middle. The 608th year uses three digits with a modern 0 in the middle.[footnote]Ibid, page 232.[/footnote] The dot as a symbol for zero also appears in a Chinese work (Chiu-chih li). The author of this document gives a strikingly clear description of how the Indian system works:Using the [Indian] numerals, multiplication and division are carried out. Each numeral is written in one stroke. When a number is counted to ten, it is advanced into the higher place. In each vacant place a dot is always put. Thus the numeral is always denoted in each place. Accordingly there can be no error in determining the place. With the numerals, calculations is easy.[footnote]Ibid, page 232.[/footnote]
Transmission to Europe
It is not completely known how the system got transmitted to Europe. Traders and travelers of the Mediterranean coast may have carried it there. It is found in a tenth-century Spanish manuscript and may have been introduced to Spain by the Arabs, who invaded the region in 711 CE and were there until 1492. In many societies, a division formed between those who used numbers and calculation for practical, every day business and those who used them for ritualistic purposes or for state business.[footnote]McLeish, p. 18[/footnote] The former might often use older systems while the latter were inclined to use the newer, more elite written numbers. Competition between the two groups arose and continued for quite some time. Figure 15.
Figure 15.The Development and Use of Different Number Bases
Introduction and Basics
During the previous discussions, we have been referring to positional base systems. In this section of the chapter, we will explore exactly what a base system is and what it means if a system is “positional.” We will do so by first looking at our own familiar, base-ten system and then deepen our exploration by looking at other possible base systems. In the next part of this section, we will journey back to Mayan civilization and look at their unique base system, which is based on the number 20 rather than the number 10. A base system is a structure within which we count. The easiest way to describe a base system is to think about our own base-ten system. The base-ten system, which we call the “decimal” system, requires a total of ten different symbols/digits to write any number. They are, of course, 0, 1, 2, . . . , 9. The decimal system is also an example of a positional base system, which simply means that the position of a digit gives its place value. Not all civilizations had a positional system even though they did have a base with which they worked. In our base-ten system, a number like 5,783,216 has meaning to us because we are familiar with the system and its places. As we know, there are six ones, since there is a 6 in the ones place. Likewise, there are seven “hundred thousands,” since the 7 resides in that place. Each digit has a value that is explicitly determined by its position within the number. We make a distinction between digit, which is just a symbol such as 5, and a number, which is made up of one or more digits. We can take this number and assign each of its digits a value. One way to do this is with a table, which follows:| 5,000,000 | = 5 × 1,000,000 | = 5 × 106 | Five million |
| +700,000 | = 7 × 100,000 | = 7 × 105 | Seven hundred thousand |
| +80,000 | = 8 × 10,000 | = 8 × 104 | Eighty thousand |
| +3,000 | = 3 × 1000 | = 3 × 103 | Three thousand |
| +200 | = 2 × 100 | = 2 × 102 | Two hundred |
| +10 | = 1 × 10 | = 1 × 101 | Ten |
| +6 | = 6 × 1 | = 6 × 100 | Six |
| 5,783,216 | Five million, seven hundred eighty-three thousand, two hundred sixteen | ||
Other Bases
For example, let’s suppose we adopt a base-five system. The only modern digits we would need for this system are 0,1,2,3 and 4. What are the place values in such a system? To answer that, we start with the ones place, as most base systems do. However, if we were to count in this system, we could only get to four (4) before we had to jump up to the next place. Our base is 5, after all! What is that next place that we would jump to? It would not be tens, since we are no longer in base-ten. We’re in a different numerical world. As the base-ten system progresses from 100 to 101, so the base-five system moves from 50 to 51 = 5. Thus, we move from the ones to the fives. After the fives, we would move to the 52 place, or the twenty fives. Note that in base-ten, we would have gone from the tens to the hundreds, which is, of course, 102. Let’s take an example and build a table. Consider the number 30412 in base five. We will write this as 304125, where the subscript 5 is not part of the number but indicates the base we’re using. First off, note that this is NOT the number “thirty thousand, four hundred twelve.” We must be careful not to impose the base-ten system on this number. Here’s what our table might look like. We will use it to convert this number to our more familiar base-ten system.| Base 5 | This column coverts to base-ten | In Base-Ten | |
| 3 × 54 | = 3 × 625 | = 1875 | |
| + | 0 × 53 | = 0 × 125 | = 0 |
| + | 4 × 52 | = 4 × 25 | = 100 |
| + | 1 × 51 | = 1 × 5 | = 5 |
| + | 2 × 50 | = 2 × 1 | = 2 |
| Total | 1982 |
Example
Convert 62347 to a base 10 number.Answer: We first note that we are given a base-7 number that we are to convert. Thus, our places will start at the ones (70), and then move up to the 7s, 49s (72), etc. Here’s the breakdown:
| Base 7 | Convert | Base 10 | |
| = 6 × 73 | = 6 × 343 | = 2058 | |
| + | = 2 × 72 | = 2 × 49 | = 98 |
| + | = 3 × 7 | = 3 × 7 | = 21 |
| + | = 4 × 1 | = 4 × 1 | = 4 |
| Total | 2181 |
try it now
Convert 410657 to a base 10 number.Answer: [latex]41065_{7} = 9994[/latex]_{10}
The Mayan Numeral System
Background
As you might imagine, the development of a base system is an important step in making the counting process more efficient. Our own base-ten system probably arose from the fact that we have 10 fingers (including thumbs) on two hands. This is a natural development. However, other civilizations have had a variety of bases other than ten. For example, the Natives of Queensland used a base-two system, counting as follows: “one, two, two and one, two two’s, much.” Some Modern South American Tribes have a base-five system counting in this way: “one, two, three, four, hand, hand and one, hand and two,” and so on. The Babylonians used a base-sixty (sexigesimal) system. In this chapter, we wrap up with a specific example of a civilization that actually used a base system other than 10.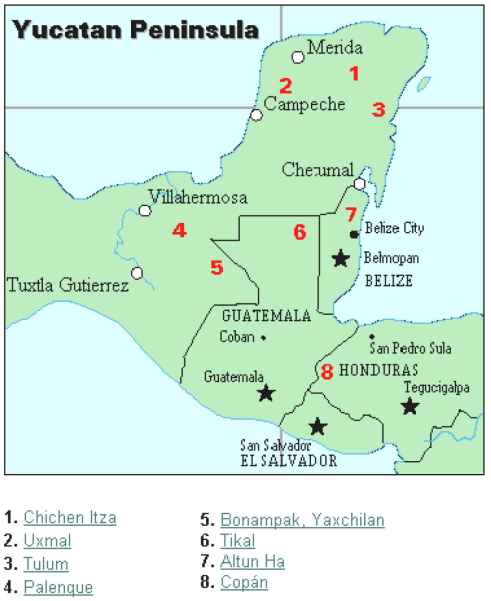 The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16[footnote]http://www.gorp.com/gorp/location/latamer/map_maya.htm[/footnote]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[footnote]Bidwell, James; Mayan Arithmetic in Mathematics Teacher, Issue 74 (Nov., 1967), p. 762–68.[/footnote] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16[footnote]http://www.gorp.com/gorp/location/latamer/map_maya.htm[/footnote]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[footnote]Bidwell, James; Mayan Arithmetic in Mathematics Teacher, Issue 74 (Nov., 1967), p. 762–68.[/footnote] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
 There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] like the sample to the left[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.
There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] like the sample to the left[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.
| Powers | Base-Ten Value | Place Name |
| 207 | 12,800,000,000 | Hablat |
| 206 | 64,000,000 | Alau |
| 205 | 3,200,000 | Kinchil |
| 204 | 160,000 | Cabal |
| 203 | 8,000 | Pic |
| 202 | 400 | Bak |
| 201 | 20 | Kal |
| 200 | 1 | Hun |
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system. As we stated earlier, the Mayans used a base-20 system, called the “vigesimal” system. Like our system, it is positional, meaning that the position of a numeric symbol indicates its place value. In the following table you can see the place value in its vertical format.[footnote]Bidwell[/footnote]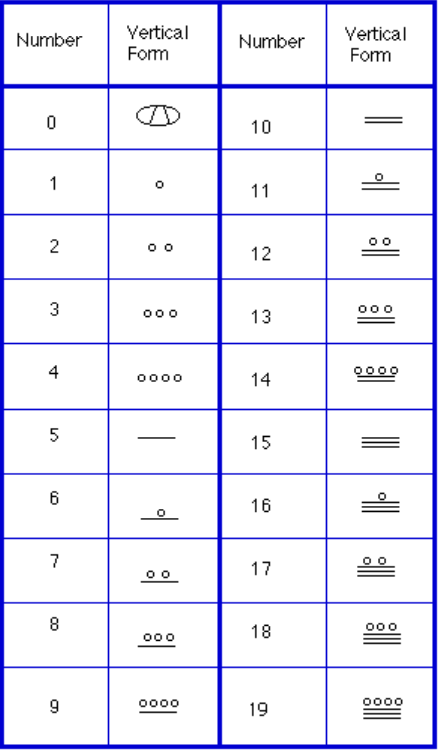 In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity 5, a dot represented the quantity 1, and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first 20 numbers are shown in the table to the right.[footnote]http://www.vpds.wsu.edu/fair_95/gym/UM001.html[/footnote]
Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.
When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as 10 getting converted to a 1 in the next place up when we carry during addition.
In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity 5, a dot represented the quantity 1, and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first 20 numbers are shown in the table to the right.[footnote]http://www.vpds.wsu.edu/fair_95/gym/UM001.html[/footnote]
Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.
When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as 10 getting converted to a 1 in the next place up when we carry during addition.
Example
What is the value of this number, which is shown in vertical form?Answer:
Starting from the bottom, we have the ones place. There are two bars and three dots in this place. Since each bar is worth 5, we have 13 ones when we count the three dots in the ones place. Looking to the place value above it (the twenties places), we see there are three dots so we have three twenties.
 Hence we can write this number in base-ten as:
(3 × 201) + (13 × 200) = (3 × 201) + (13 × 1) = 60 + 13 = 73
Hence we can write this number in base-ten as:
(3 × 201) + (13 × 200) = (3 × 201) + (13 × 1) = 60 + 13 = 73
Example
What is the value of the following Mayan number?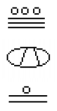
Answer: This number has 11 in the ones place, zero in the 20s place, and 18 in the 202 = 400s place. Hence, the value of this number in base-ten is: 18 × 400 + 0 × 20 + 11 × 1 = 7211.
try it now
Convert the Mayan number below to base 10.
Answer:
Answer: [latex]5617_{10} = 14,0,17_{20}[/latex]. Note that there is a zero in the 20’s place, so you’ll need to use the appropriate zero symbol in between the ones and 400’s places.
![]()
 [footnote]http://forum.swarthmore.edu/k12/mayan.math/mayan2.html[/footnote]
[footnote]http://forum.swarthmore.edu/k12/mayan.math/mayan2.html[/footnote]
 Next, put all of the symbols from both numbers into a single set of places (boxes), and to the right of this new number draw a set of empty boxes where you will place the final sum:
Next, put all of the symbols from both numbers into a single set of places (boxes), and to the right of this new number draw a set of empty boxes where you will place the final sum:
 You are now ready to start carrying. Begin with the place that has the lowest value, just as you do with Arabic numbers. Start at the bottom place, where each dot is worth 1. There are six dots, but a maximum of four are allowed in any one place; once you get to five dots, you must convert to a bar. Since five dots make one bar, we draw a bar through five of the dots, leaving us with one dot which is under the four-dot limit. Put this dot into the bottom place of the empty set of boxes you just drew:
You are now ready to start carrying. Begin with the place that has the lowest value, just as you do with Arabic numbers. Start at the bottom place, where each dot is worth 1. There are six dots, but a maximum of four are allowed in any one place; once you get to five dots, you must convert to a bar. Since five dots make one bar, we draw a bar through five of the dots, leaving us with one dot which is under the four-dot limit. Put this dot into the bottom place of the empty set of boxes you just drew:
 Now look at the bars in the bottom place. There are five, and the maximum number the place can hold is three. Four bars are equal to one dot in the next highest place.
Whenever we have four bars in a single place we will automatically convert that to a dot in the next place up. We draw a circle around four of the bars and an arrow up to the dots' section of the higher place. At the end of that arrow, draw a new dot. That dot represents 20 just the same as the other dots in that place. Not counting the circled bars in the bottom place, there is one bar left. One bar is under the three-bar limit; put it under the dot in the set of empty places to the right.
Now look at the bars in the bottom place. There are five, and the maximum number the place can hold is three. Four bars are equal to one dot in the next highest place.
Whenever we have four bars in a single place we will automatically convert that to a dot in the next place up. We draw a circle around four of the bars and an arrow up to the dots' section of the higher place. At the end of that arrow, draw a new dot. That dot represents 20 just the same as the other dots in that place. Not counting the circled bars in the bottom place, there is one bar left. One bar is under the three-bar limit; put it under the dot in the set of empty places to the right.
 Now there are only three dots in the next highest place, so draw them in the corresponding empty box.
Now there are only three dots in the next highest place, so draw them in the corresponding empty box.
 We can see here that we have 3 twenties (60), and 6 ones, for a total of 66. We check and note that 37 + 29 = 66, so we have done this addition correctly. Is it easier to just do it in base-ten? Probably, but that’s only because it’s more familiar to you. Your task here is to try to learn a new base system and how addition can be done in slightly different ways than what you have seen in the past. Note, however, that the concept of carrying is still used, just as it is in our own addition algorithm.
We can see here that we have 3 twenties (60), and 6 ones, for a total of 66. We check and note that 37 + 29 = 66, so we have done this addition correctly. Is it easier to just do it in base-ten? Probably, but that’s only because it’s more familiar to you. Your task here is to try to learn a new base system and how addition can be done in slightly different ways than what you have seen in the past. Note, however, that the concept of carrying is still used, just as it is in our own addition algorithm.


