Binomial Theorem
Identifying Binomial Coefficients
In Counting Principles, we studied combinations. In the shortcut to finding [latex]{\left(x+y\right)}^{n}[/latex], we will need to use combinations to find the coefficients that will appear in the expansion of the binomial. In this case, we use the notation [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] instead of [latex]C\left(n,r\right)[/latex], but it can be calculated in the same way. So[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]
The combination [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] is called a binomial coefficient. An example of a binomial coefficient is [latex]\left(\begin{array}{c}5\\ 2\end{array}\right)=C\left(5,2\right)=10[/latex].
A General Note: Binomial Coefficients
If [latex]n[/latex] and [latex]r[/latex] are integers greater than or equal to 0 with [latex]n\ge r[/latex], then the binomial coefficient is[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]
Q & A
Is a binomial coefficient always a whole number?
Yes. Just as the number of combinations must always be a whole number, a binomial coefficient will always be a whole number.Example 1: Finding Binomial Coefficients
Find each binomial coefficient.- [latex]\left(\begin{array}{c}5\\ 3\end{array}\right)[/latex]
- [latex]\left(\begin{array}{c}9\\ 2\end{array}\right)[/latex]
- [latex]\left(\begin{array}{c}9\\ 7\end{array}\right)[/latex]
Solution
Use the formula to calculate each binomial coefficient. You can also use the [latex]{n}_{}{C}_{r}[/latex] function on your calculator.[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=C\left(n,r\right)=\frac{n!}{r!\left(n-r\right)!}[/latex]
- [latex]\left(\begin{array}{c}5\\ 3\end{array}\right)=\frac{5!}{3!\left(5 - 3\right)!}=\frac{5\cdot 4\cdot 3!}{3!2!}=10[/latex]
- [latex]\left(\begin{array}{c}9\\ 2\end{array}\right)=\frac{9!}{2!\left(9 - 2\right)!}=\frac{9\cdot 8\cdot 7!}{2!7!}=36[/latex]
- [latex]\left(\begin{array}{c}9\\ 7\end{array}\right)=\frac{9!}{7!\left(9 - 7\right)!}=\frac{9\cdot 8\cdot 7!}{7!2!}=36[/latex]
Analysis of the Solution
Notice that we obtained the same result for parts (b) and (c). If you look closely at the solution for these two parts, you will see that you end up with the same two factorials in the denominator, but the order is reversed, just as with combinations.[latex]\left(\begin{array}{c}n\\ r\end{array}\right)=\left(\begin{array}{c}n\\ n-r\end{array}\right)[/latex]
Try It 1
Find each binomial coefficient.a. [latex]\left(\begin{array}{c}7\\ 3\end{array}\right)[/latex]
b. [latex]\left(\begin{array}{c}11\\ 4\end{array}\right)[/latex]
Solution
Using the Binomial Theorem
When we expand [latex]{\left(x+y\right)}^{n}[/latex] by multiplying, the result is called a binomial expansion, and it includes binomial coefficients. If we wanted to expand [latex]{\left(x+y\right)}^{52}[/latex], we might multiply [latex]\left(x+y\right)[/latex] by itself fifty-two times. This could take hours! If we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions.[latex]\begin{array}{l}{\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2}\hfill \\ {\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\hfill \\ {\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}\hfill \end{array}[/latex]
First, let’s examine the exponents. With each successive term, the exponent for [latex]x[/latex] decreases and the exponent for [latex]y[/latex] increases. The sum of the two exponents is [latex]n[/latex] for each term.
Next, let’s examine the coefficients. Notice that the coefficients increase and then decrease in a symmetrical pattern. The coefficients follow a pattern:
[latex]\left(\begin{array}{c}n\\ 0\end{array}\right),\left(\begin{array}{c}n\\ 1\end{array}\right),\left(\begin{array}{c}n\\ 2\end{array}\right),...,\left(\begin{array}{c}n\\ n\end{array}\right)[/latex].
These patterns lead us to the Binomial Theorem, which can be used to expand any binomial.
[latex]\begin{array}{ll}{\left(x+y\right)}^{n}\hfill & =\sum _{k=0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}\hfill \\ \hfill & ={x}^{n}+\left(\begin{array}{c}n\\ 1\end{array}\right){x}^{n - 1}y+\left(\begin{array}{c}n\\ 2\end{array}\right){x}^{n - 2}{y}^{2}+...+\left(\begin{array}{c}n\\ n - 1\end{array}\right)x{y}^{n - 1}+{y}^{n}\hfill \end{array}[/latex]
Another way to see the coefficients is to examine the expansion of a binomial in general form, [latex]x+y[/latex], to successive powers 1, 2, 3, and 4.
[latex]\begin{array}{l}{\left(x+y\right)}^{1}=x+y\hfill \\ {\left(x+y\right)}^{2}={x}^{2}+2xy+{y}^{2}\hfill \\ {\left(x+y\right)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\hfill \\ {\left(x+y\right)}^{4}={x}^{4}+4{x}^{3}y+6{x}^{2}{y}^{2}+4x{y}^{3}+{y}^{4}\hfill \end{array}[/latex]
Can you guess the next expansion for the binomial [latex]{\left(x+y\right)}^{5}?[/latex]
 Figure 1
Figure 1- There are [latex]n+1[/latex] terms in the expansion of [latex]{\left(x+y\right)}^{n}[/latex].
- The degree (or sum of the exponents) for each term is [latex]n[/latex].
- The powers on [latex]x[/latex] begin with [latex]n[/latex] and decrease to 0.
- The powers on [latex]y[/latex] begin with 0 and increase to [latex]n[/latex].
- The coefficients are symmetric.
- Introduce [latex]{x}^{5}[/latex], and then for each successive term reduce the exponent on [latex]x[/latex] by 1 until [latex]{x}^{0}=1[/latex] is reached.
- Introduce [latex]{y}^{0}=1[/latex], and then increase the exponent on [latex]y[/latex] by 1 until [latex]{y}^{5}[/latex] is reached.
[latex]{x}^{5},{x}^{4}y,{x}^{3}{y}^{2},{x}^{2}{y}^{3},x{y}^{4},{y}^{5}[/latex]
[latex]{\left(x+y\right)}^{5}={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}[/latex].
But where do those coefficients come from? The binomial coefficients are symmetric. We can see these coefficients in an array known as Pascal's Triangle, shown in Figure 2.
 Figure 2
Figure 2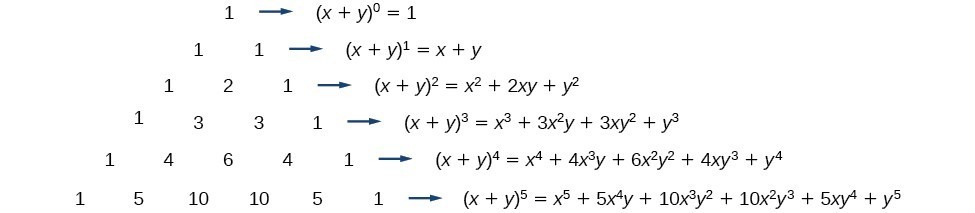
A General Note: The Binomial Theorem
The Binomial Theorem is a formula that can be used to expand any binomial.[latex]\begin{array}{ll}{\left(x+y\right)}^{n}\hfill & =\sum _{k=0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}\hfill \\ \hfill & ={x}^{n}+\left(\begin{array}{c}n\\ 1\end{array}\right){x}^{n - 1}y+\left(\begin{array}{c}n\\ 2\end{array}\right){x}^{n - 2}{y}^{2}+...+\left(\begin{array}{c}n\\ n - 1\end{array}\right)x{y}^{n - 1}+{y}^{n}\hfill \end{array}[/latex]
How To: Given a binomial, write it in expanded form.
- Determine the value of [latex]n[/latex] according to the exponent.
- Evaluate the [latex]k=0[/latex] through [latex]k=n[/latex] using the Binomial Theorem formula.
- Simplify.
Example 2: Expanding a Binomial
Write in expanded form.- [latex]{\left(x+y\right)}^{5}[/latex]
- [latex]{\left(3x-y\right)}^{4}[/latex]
Solution
- Substitute [latex]n=5[/latex] into the formula. Evaluate the [latex]k=0[/latex] through [latex]k=5[/latex] terms. Simplify.
[latex]\begin{array}{ll}{\left(x+y\right)}^{5}\hfill & =\left(\begin{array}{c}5\\ 0\end{array}\right){x}^{5}{y}^{0}+\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}{y}^{1}+\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}+\left(\begin{array}{c}5\\ 3\end{array}\right){x}^{2}{y}^{3}+\left(\begin{array}{c}5\\ 4\end{array}\right){x}^{1}{y}^{4}+\left(\begin{array}{c}5\\ 5\end{array}\right){x}^{0}{y}^{5}\hfill \\ {\left(x+y\right)}^{5}\hfill & ={x}^{5}+5{x}^{4}y+10{x}^{3}{y}^{2}+10{x}^{2}{y}^{3}+5x{y}^{4}+{y}^{5}\hfill \end{array}[/latex]
- Substitute [latex]n=4[/latex] into the formula. Evaluate the [latex]k=0[/latex] through [latex]k=4[/latex] terms. Notice that [latex]3x[/latex] is in the place that was occupied by [latex]x[/latex] and that [latex]-y[/latex] is in the place that was occupied by [latex]y[/latex]. So we substitute them. Simplify.
[latex]\begin{array}{ll}{\left(3x-y\right)}^{4}\hfill & =\left(\begin{array}{c}4\\ 0\end{array}\right){\left(3x\right)}^{4}{\left(-y\right)}^{0}+\left(\begin{array}{c}4\\ 1\end{array}\right){\left(3x\right)}^{3}{\left(-y\right)}^{1}+\left(\begin{array}{c}4\\ 2\end{array}\right){\left(3x\right)}^{2}{\left(-y\right)}^{2}+\left(\begin{array}{c}4\\ 3\end{array}\right){\left(3x\right)}^{1}{\left(-y\right)}^{3}+\left(\begin{array}{c}4\\ 4\end{array}\right){\left(3x\right)}^{0}{\left(-y\right)}^{4}\hfill \\ {\left(3x-y\right)}^{4}\hfill & =81{x}^{4}-108{x}^{3}y+54{x}^{2}{y}^{2}-12x{y}^{3}+{y}^{4}\hfill \end{array}[/latex]
Analysis of the Solution
Notice the alternating signs in part b. This happens because [latex]\left(-y\right)[/latex] raised to odd powers is negative, but [latex]\left(-y\right)[/latex] raised to even powers is positive. This will occur whenever the binomial contains a subtraction sign.Try It 2
Write in expanded form.a. [latex]{\left(x-y\right)}^{5}[/latex]
b. [latex]{\left(2x+5y\right)}^{3}[/latex]
Solution
Using the Binomial Theorem to Find a Single Term
Expanding a binomial with a high exponent such as [latex]{\left(x+2y\right)}^{16}[/latex] can be a lengthy process. Sometimes we are interested only in a certain term of a binomial expansion. We do not need to fully expand a binomial to find a single specific term. Note the pattern of coefficients in the expansion of [latex]{\left(x+y\right)}^{5}[/latex].[latex]{\left(x+y\right)}^{5}={x}^{5}+\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}y+\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}+\left(\begin{array}{c}5\\ 3\end{array}\right){x}^{2}{y}^{3}+\left(\begin{array}{c}5\\ 4\end{array}\right)x{y}^{4}+{y}^{5}[/latex]
The second term is [latex]\left(\begin{array}{c}5\\ 1\end{array}\right){x}^{4}y[/latex]. The third term is [latex]\left(\begin{array}{c}5\\ 2\end{array}\right){x}^{3}{y}^{2}[/latex]. We can generalize this result.
[latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]
A General Note: The (r+1)th Term of a Binomial Expansion
The [latex]\left(r+1\right)\text{th}[/latex] term of the binomial expansion of [latex]{\left(x+y\right)}^{n}[/latex] is:[latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]
How To: Given a binomial, write a specific term without fully expanding.
- Determine the value of [latex]n[/latex] according to the exponent.
- Determine [latex]\left(r+1\right)[/latex].
- Determine [latex]r[/latex].
- Replace [latex]r[/latex] in the formula for the [latex]\left(r+1\right)\text{th}[/latex] term of the binomial expansion.
Example 3: Writing a Given Term of a Binomial Expansion
Find the tenth term of [latex]{\left(x+2y\right)}^{16}[/latex] without fully expanding the binomial.Solution
Because we are looking for the tenth term, [latex]r+1=10[/latex], we will use [latex]r=9[/latex] in our calculations.[latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex]
[latex]\left(\begin{array}{c}16\\ 9\end{array}\right){x}^{16 - 9}{\left(2y\right)}^{9}=5\text{,}857\text{,}280{x}^{7}{y}^{9}[/latex]
Try It 3
Find the sixth term of [latex]{\left(3x-y\right)}^{9}[/latex] without fully expanding the binomial. SolutionKey Equations
| Binomial Theorem | [latex]{\left(x+y\right)}^{n}=\sum _{k - 0}^{n}\left(\begin{array}{c}n\\ k\end{array}\right){x}^{n-k}{y}^{k}[/latex] |
| [latex]\left(r+1\right)th[/latex] term of a binomial expansion | [latex]\left(\begin{array}{c}n\\ r\end{array}\right){x}^{n-r}{y}^{r}[/latex] |
Key Concepts
- [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex] is called a binomial coefficient and is equal to [latex]C\left(n,r\right)[/latex].
- The Binomial Theorem allows us to expand binomials without multiplying.
- We can find a given term of a binomial expansion without fully expanding the binomial.
Glossary
- binomial coefficient
- the number of ways to choose r objects from n objects where order does not matter; equivalent to [latex]C\left(n,r\right)[/latex], denoted [latex]\left(\begin{array}{c}n\\ r\end{array}\right)[/latex]
- binomial expansion
- the result of expanding [latex]{\left(x+y\right)}^{n}[/latex] by multiplying
- Binomial Theorem
- a formula that can be used to expand any binomial
Section Exercises
1. What is a binomial coefficient, and how it is calculated? 2. What role do binomial coefficients play in a binomial expansion? Are they restricted to any type of number? 3. What is the Binomial Theorem and what is its use? 4. When is it an advantage to use the Binomial Theorem? Explain. For the following exercises, evaluate the binomial coefficient. 5. [latex]\left(\begin{array}{c}6\\ 2\end{array}\right)[/latex] 6. [latex]\left(\begin{array}{c}5\\ 3\end{array}\right)[/latex] 7. [latex]\left(\begin{array}{c}7\\ 4\end{array}\right)[/latex] 8. [latex]\left(\begin{array}{c}9\\ 7\end{array}\right)[/latex] 9. [latex]\left(\begin{array}{c}10\\ 9\end{array}\right)[/latex] 10. [latex]\left(\begin{array}{c}25\\ 11\end{array}\right)[/latex] 11. [latex]\left(\begin{array}{c}17\\ 6\end{array}\right)[/latex] 12. [latex]\left(\begin{array}{c}200\\ 199\end{array}\right)[/latex] For the following exercises, use the Binomial Theorem to expand each binomial. 13. [latex]{\left(4a-b\right)}^{3}[/latex] 14. [latex]{\left(5a+2\right)}^{3}[/latex] 15. [latex]{\left(3a+2b\right)}^{3}[/latex] 16. [latex]{\left(2x+3y\right)}^{4}[/latex] 17. [latex]{\left(4x+2y\right)}^{5}[/latex] 18. [latex]{\left(3x - 2y\right)}^{4}[/latex] 19. [latex]{\left(4x - 3y\right)}^{5}[/latex] 20. [latex]{\left(\frac{1}{x}+3y\right)}^{5}[/latex] 21. [latex]{\left({x}^{-1}+2{y}^{-1}\right)}^{4}[/latex] 22. [latex]{\left(\sqrt{x}-\sqrt{y}\right)}^{5}[/latex] For the following exercises, use the Binomial Theorem to write the first three terms of each binomial. 23. [latex]{\left(a+b\right)}^{17}[/latex] 24. [latex]{\left(x - 1\right)}^{18}[/latex] 25. [latex]{\left(a - 2b\right)}^{15}[/latex] 26. [latex]{\left(x - 2y\right)}^{8}[/latex] 27. [latex]{\left(3a+b\right)}^{20}[/latex] 28. [latex]{\left(2a+4b\right)}^{7}[/latex] 29. [latex]{\left({x}^{3}-\sqrt{y}\right)}^{8}[/latex] For the following exercises, find the indicated term of each binomial without fully expanding the binomial. 30. The fourth term of [latex]{\left(2x - 3y\right)}^{4}[/latex] 31. The fourth term of [latex]{\left(3x - 2y\right)}^{5}[/latex] 32. The third term of [latex]{\left(6x - 3y\right)}^{7}[/latex] 33. The eighth term of [latex]{\left(7+5y\right)}^{14}[/latex] 34. The seventh term of [latex]{\left(a+b\right)}^{11}[/latex] 35. The fifth term of [latex]{\left(x-y\right)}^{7}[/latex] 36. The tenth term of [latex]{\left(x - 1\right)}^{12}[/latex] 37. The ninth term of [latex]{\left(a - 3{b}^{2}\right)}^{11}[/latex] 38. The fourth term of [latex]{\left({x}^{3}-\frac{1}{2}\right)}^{10}[/latex] 39. The eighth term of [latex]{\left(\frac{y}{2}+\frac{2}{x}\right)}^{9}[/latex] For the following exercises, use the Binomial Theorem to expand the binomial [latex]f\left(x\right)={\left(x+3\right)}^{4}[/latex]. Then find and graph each indicated sum on one set of axes. 40. Find and graph [latex]{f}_{1}\left(x\right)[/latex], such that [latex]{f}_{1}\left(x\right)[/latex] is the first term of the expansion. 41. Find and graph [latex]{f}_{2}\left(x\right)[/latex], such that [latex]{f}_{2}\left(x\right)[/latex] is the sum of the first two terms of the expansion. 42. Find and graph [latex]{f}_{3}\left(x\right)[/latex], such that [latex]{f}_{3}\left(x\right)[/latex] is the sum of the first three terms of the expansion. 43. Find and graph [latex]{f}_{4}\left(x\right)[/latex], such that [latex]{f}_{4}\left(x\right)[/latex] is the sum of the first four terms of the expansion. 44. Find and graph [latex]{f}_{5}\left(x\right)[/latex], such that [latex]{f}_{5}\left(x\right)[/latex] is the sum of the first five terms of the expansion. 45. In the expansion of [latex]{\left(5x+3y\right)}^{n}[/latex], each term has the form [latex]\left(\begin{array}{c}n\\ k\end{array}\right){a}^{n-k}{b}^{k}, \text{where} k[/latex] successively takes on the value [latex]0,1,2,...,n[/latex]. If [latex]\left(\begin{array}{c}n\\ k\end{array}\right)=\left(\begin{array}{c}7\\ 2\end{array}\right)[/latex], what is the corresponding term? 46. In the expansion of [latex]{\left(a+b\right)}^{n}[/latex], the coefficient of [latex]{a}^{n-k}{b}^{k}[/latex] is the same as the coefficient of which other term? 47. Find [latex]\left(\begin{array}{c}n\\ k - 1\end{array}\right)+\left(\begin{array}{c}n\\ k\end{array}\right)[/latex] and write the answer as a binomial coefficient in the form [latex]\left(\begin{array}{c}n\\ k\end{array}\right)[/latex]. Prove it. Hint: Use the fact that, for any integer [latex]p[/latex], such that [latex]p\ge 1,p!=p\left(p - 1\right)!\text{.}[/latex] 48. Consider the expansion of [latex]{\left(x+b\right)}^{40}[/latex]. What is the exponent of [latex]b[/latex] in the [latex]k\text{th}[/latex] term? 49. Which expression cannot be expanded using the Binomial Theorem? Explain.- [latex]\left({x}^{2}-2x+1\right)[/latex]
- [latex]{\left(\sqrt{a}+4\sqrt{a}-5\right)}^{8}[/latex]
- [latex]{\left({x}^{3}+2{y}^{2}-z\right)}^{5}[/latex]
- [latex]{\left(3{x}^{2}-\sqrt{2{y}^{3}}\right)}^{12}[/latex]
Licenses & Attributions
CC licensed content, Original
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
