The Other Trigonometric Functions
Find exact values of the trigonometric functions secant, cosecant, tangent, and cotangent
To define the remaining functions, we will once again draw a unit circle with a point [latex]\left(x,y\right)[/latex] corresponding to an angle of [latex]t[/latex], as shown in Figure 1. As with the sine and cosine, we can use the [latex]\left(x,y\right)[/latex] coordinates to find the other functions. Figure 1
Figure 1- The secant function is the reciprocal of the cosine function. In Figure 1, the secant of angle [latex]t[/latex] is equal to [latex]\frac{1}{\cos t}=\frac{1}{x},x\ne 0\\[/latex]. The secant function is abbreviated as [latex]\text{sec}\text{.}\\[/latex]
- The cotangent function is the reciprocal of the tangent function. In Figure 1, the cotangent of angle [latex]t[/latex] is equal to [latex]\frac{\cos t}{\sin t}=\frac{x}{y},y\ne 0\\[/latex]. The cotangent function is abbreviated as [latex]\text{cot}\text{.}\\[/latex]
- The cosecant function is the reciprocal of the sine function. In Figure 1, the cosecant of angle [latex]t[/latex] is equal to [latex]\frac{1}{\sin t}=\frac{1}{y},y\ne 0\\[/latex]. The cosecant function is abbreviated as [latex]\text{csc}\text{.}\\[/latex]
A General Note: Tangent, Secant, Cosecant, and Cotangent Functions
If [latex]t[/latex] is a real number and [latex]\left(x,y\right)[/latex] is a point where the terminal side of an angle of [latex]t[/latex] radians intercepts the unit circle, then[latex]\begin{array}{l}\tan t=\frac{y}{x},x\ne 0\\ \sec t=\frac{1}{x},x\ne 0\\ \csc t=\frac{1}{y},y\ne 0\\ \cot t=\frac{x}{y},y\ne 0\end{array}\\[/latex]
Example 1: Finding Trigonometric Functions from a Point on the Unit Circle
The point [latex]\left(-\frac{\sqrt{3}}{2},\frac{1}{2}\right)\\[/latex] is on the unit circle, as shown in Figure 2. Find [latex]\sin t,\cos t,\tan t,\sec t,\csc t[/latex], and [latex]\cot t\\[/latex]. Figure 2
Figure 2Solution
Because we know the [latex]\left(x,y\right)[/latex] coordinates of the point on the unit circle indicated by angle [latex]t[/latex], we can use those coordinates to find the six functions:[latex]\begin{array}{l}\sin t=y=\frac{1}{2}\\ \cos t=x=-\frac{\sqrt{3}}{2}\\ \tan t=\frac{y}{x}=\frac{\frac{1}{2}}{-\frac{\sqrt{3}}{2}}=\frac{1}{2}\left(-\frac{2}{\sqrt{3}}\right)=-\frac{1}{\sqrt{3}}=-\frac{\sqrt{3}}{3}\\ \sec t=\frac{1}{x}=\frac{1}{\frac{-\frac{\sqrt{3}}{2}}{}}=-\frac{2}{\sqrt{3}}=-\frac{2\sqrt{3}}{3}\\ \csc t=\frac{1}{y}=\frac{1}{\frac{1}{2}}=2\\ \cot t=\frac{x}{y}=\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}=-\frac{\sqrt{3}}{2}\left(\frac{2}{1}\right)=-\sqrt{3}\end{array}\\[/latex]
Try It 1
The point [latex]\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)\\[/latex] is on the unit circle, as shown in Figure 3. Find [latex]\sin t,\cos t,\tan t,\sec t,\csc t\\[/latex], and [latex]\cot t\\[/latex].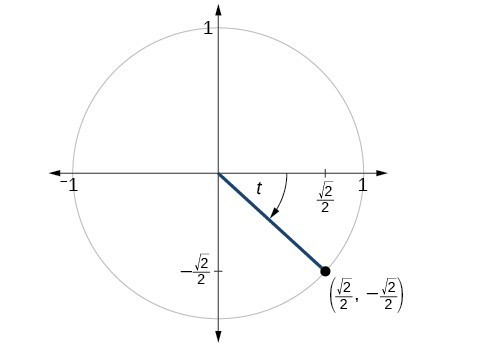 Figure 3
Figure 3Example 2: Finding the Trigonometric Functions of an Angle
Find [latex]\sin t,\cos t,\tan t,\sec t,\csc t\\[/latex], and [latex]\cot t\\[/latex] when [latex]t=\frac{\pi }{6}\\[/latex].Solution
We have previously used the properties of equilateral triangles to demonstrate that [latex]\sin \frac{\pi }{6}=\frac{1}{2}\\[/latex] and [latex]\cos \frac{\pi }{6}=\frac{\sqrt{3}}{2}\\[/latex]. We can use these values and the definitions of tangent, secant, cosecant, and cotangent as functions of sine and cosine to find the remaining function values.[latex]\begin{array}{l}\begin{array}{l}\\ \tan \text{ }\frac{\pi }{6}=\frac{\sin \text{ }\frac{\pi }{6}}{\cos \text{ }\frac{\pi }{6}}\end{array}\hfill \\ =\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\hfill \end{array}\\[/latex]
[latex]\begin{array}{l}\sec \frac{\pi }{6}=\frac{1}{\cos \frac{\pi }{6}}\hfill \\ =\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}\hfill \end{array}\\[/latex]
[latex]\csc \frac{\pi }{6}=\frac{1}{\sin \frac{\pi }{6}}=\frac{1}{\frac{1}{2}}=2\\[/latex]
[latex]\begin{array}{l}\cot \frac{\pi }{6}=\frac{\cos \frac{\pi }{6}}{\sin \frac{\pi }{6}}\hfill \\ =\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}\hfill \end{array}\\[/latex]
Try It 2
Find [latex]\sin t,\cos t,\tan t,\sec t,\csc t[/latex], and [latex]\cot t[/latex] when [latex]t=\frac{\pi }{3}[/latex]. Solution| Angle | [latex]0[/latex] | [latex]\frac{\pi }{6},\text{ or }{30}^{\circ}\\[/latex] | [latex]\frac{\pi }{4},\text{ or } {45}^{\circ }\\[/latex] | [latex]\frac{\pi }{3},\text{ or }{60}^{\circ }\\[/latex] | [latex]\frac{\pi }{2},\text{ or }{90}^{\circ }\\[/latex] |
| Cosine | 1 | [latex]\frac{\sqrt{3}}{2}\\[/latex] | [latex]\frac{\sqrt{2}}{2}\\[/latex] | [latex]\frac{1}{2}\\[/latex] | 0 |
| Sine | 0 | [latex]\frac{1}{2}\\[/latex] | [latex]\frac{\sqrt{2}}{2}\\[/latex] | [latex]\frac{\sqrt{3}}{2}\\[/latex] | 1 |
| Tangent | 0 | [latex]\frac{\sqrt{3}}{3}\\[/latex] | 1 | [latex]\sqrt{3}\\[/latex] | Undefined |
| Secant | 1 | [latex]\frac{2\sqrt{3}}{3}\\[/latex] | [latex]\sqrt{2}\\[/latex] | 2 | Undefined |
| Cosecant | Undefined | 2 | [latex]\sqrt{2}\\[/latex] | [latex]\frac{2\sqrt{3}}{3}\\[/latex] | 1 |
| Cotangent | Undefined | [latex]\sqrt{3}\\[/latex] | 1 | [latex]\frac{\sqrt{3}}{3}\\[/latex] | 0 |
Using Reference Angles to Evaluate Tangent, Secant, Cosecant, and Cotangent
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same: Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x- and y-values in the original quadrant. Figure 4 shows which functions are positive in which quadrant. To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase "A Smart Trig Class." Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is "A," all of the six trigonometric functions are positive. In quadrant II, "Smart," only sine and its reciprocal function, cosecant, are positive. In quadrant III, "Trig," only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, "Class," only cosine and its reciprocal function, secant, are positive. Figure 4
Figure 4How To: Given an angle not in the first quadrant, use reference angles to find all six trigonometric functions.
- Measure the angle formed by the terminal side of the given angle and the horizontal axis. This is the reference angle.
- Evaluate the function at the reference angle.
- Observe the quadrant where the terminal side of the original angle is located. Based on the quadrant, determine whether the output is positive or negative.
Example 3: Using Reference Angles to Find Trigonometric Functions
Use reference angles to find all six trigonometric functions of [latex]-\frac{5\pi }{6}[/latex].Solution
The angle between this angle’s terminal side and the x-axis is [latex]\frac{\pi }{6}[/latex], so that is the reference angle. Since [latex]-\frac{5\pi }{6}[/latex] is in the third quadrant, where both [latex]x[/latex] and [latex]y[/latex] are negative, cosine, sine, secant, and cosecant will be negative, while tangent and cotangent will be positive.[latex]\begin{array}{l}\cos \left(-\frac{5\pi }{6}\right)=-\frac{\sqrt{3}}{2},\sin \left(-\frac{5\pi }{6}\right)=-\frac{1}{2},\text{tan}\left(-\frac{5\pi }{6}\right)=\frac{\sqrt{3}}{3}\hfill \\ \text{sec}\left(-\frac{5\pi }{6}\right)=-\frac{2\sqrt{3}}{3},\text{csc}\left(-\frac{5\pi }{6}\right)=-2,\cot \left(-\frac{5\pi }{6}\right)=\sqrt{3}\hfill \end{array}[/latex]
Try It 3
Use reference angles to find all six trigonometric functions of [latex]-\frac{7\pi }{4}[/latex]. SolutionUsing Even and Odd Trigonometric Functions
To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard. Consider the function [latex]f\left(x\right)={x}^{2}[/latex], shown in Figure 5. The graph of the function is symmetrical about the y-axis. All along the curve, any two points with opposite x-values have the same function value. This matches the result of calculation: [latex]{\left(4\right)}^{2}={\left(-4\right)}^{2}[/latex], [latex]{\left(-5\right)}^{2}={\left(5\right)}^{2}[/latex], and so on. So [latex]f\left(x\right)={x}^{2}[/latex] is an even function, a function such that two inputs that are opposites have the same output. That means [latex]f\left(-x\right)=f\left(x\right)[/latex].
Figure 5. The function [latex]f\left(x\right)={x}^{2}[/latex] is an even function.
Now consider the function [latex]f\left(x\right)={x}^{3}[/latex], shown in Figure 6. The graph is not symmetrical about the y-axis. All along the graph, any two points with opposite x-values also have opposite y-values. So [latex]f\left(x\right)={x}^{3}[/latex] is an odd function, one such that two inputs that are opposites have outputs that are also opposites. That means [latex]f\left(-x\right)=-f\left(x\right)[/latex].
Figure 6. The function [latex]f\left(x\right)={x}^{3}[/latex] is an odd function.
We can test whether a trigonometric function is even or odd by drawing a unit circle with a positive and a negative angle, as in Figure 7. The sine of the positive angle is [latex]y[/latex]. The sine of the negative angle is −y. The sine function, then, is an odd function. We can test each of the six trigonometric functions in this fashion. The results are shown in in the table below. Figure 7
Figure 7| [latex]\begin{array}{l}\sin t=y\hfill \\ \sin \left(-t\right)=-y\hfill \\ \sin t\ne \sin \left(-t\right)\hfill \end{array}[/latex] | [latex]\begin{array}{l}\text{cos}t=x\hfill \\ \cos \left(-t\right)=x\hfill \\ \cos t=\cos \left(-t\right)\hfill \end{array}[/latex] | [latex]\begin{array}{l}\text{tan}\left(t\right)=\frac{y}{x}\hfill \\ \tan \left(-t\right)=-\frac{y}{x}\hfill \\ \tan t\ne \tan \left(-t\right)\hfill \end{array}[/latex] |
| [latex]\begin{array}{l}\sec t=\frac{1}{x}\hfill \\ \sec \left(-t\right)=\frac{1}{x}\hfill \\ \sec t=\sec \left(-t\right)\hfill \end{array}[/latex] | [latex]\begin{array}{l}\csc t=\frac{1}{y}\hfill \\ \csc \left(-t\right)=\frac{1}{-y}\hfill \\ \csc t\ne \csc \left(-t\right)\hfill \end{array}[/latex] | [latex]\begin{array}{l}\cot t=\frac{x}{y}\hfill \\ \cot \left(-t\right)=\frac{x}{-y}\hfill \\ \cot t\ne cot\left(-t\right)\hfill \end{array}[/latex] |
A General Note: Even and Odd Trigonometric Functions
An even function is one in which [latex]f\left(-x\right)=f\left(x\right)[/latex]. An odd function is one in which [latex]f\left(-x\right)=-f\left(x\right)[/latex]. Cosine and secant are even:[latex]\begin{array}{l}\cos \left(-t\right)=\text{cos}t\hfill \\ \sec \left(-t\right)=\sec t\hfill \end{array}[/latex]
Sine, tangent, cosecant, and cotangent are odd:
[latex]\begin{array}{l}\sin \left(-t\right)=-\sin t\hfill \\ \tan \left(-t\right)=-\tan t\hfill \\ \csc \left(-t\right)=-\csc t\hfill \\ \cot \left(-t\right)=-\cot t\hfill \end{array}[/latex]
Example 4: Using Even and Odd Properties of Trigonometric Functions
If the secant of angle [latex]t[/latex] is 2, what is the secant of [latex]-t?[/latex]Solution
Secant is an even function. The secant of an angle is the same as the secant of its opposite. So if the secant of angle t is 2, the secant of [latex]-t[/latex] is also 2.Try It 4
If the cotangent of angle [latex]t[/latex] is [latex]\sqrt{3}[/latex], what is the cotangent of [latex]-t?[/latex] SolutionRecognize and Use Fundamental Identities
We have explored a number of properties of trigonometric functions. Now, we can take the relationships a step further, and derive some fundamental identities. Identities are statements that are true for all values of the input on which they are defined. Usually, identities can be derived from definitions and relationships we already know. For example, the Pythagorean Identity we learned earlier was derived from the Pythagorean Theorem and the definitions of sine and cosine.A General Note: Fundamental Identities
We can derive some useful identities from the six trigonometric functions. The other four trigonometric functions can be related back to the sine and cosine functions using these basic relationships:[latex]\text{tan}t=\frac{\sin t}{\cos t}\\[/latex]
[latex]\sec t=\frac{1}{\cos t}\\[/latex]
[latex]\csc t=\frac{1}{\sin t}\\[/latex]
[latex]\text{cot}t=\frac{1}{\text{tan}t}=\frac{\text{cos}t}{\text{sin}t}\\[/latex]
Example 5: Using Identities to Evaluate Trigonometric Functions
- Given [latex]\sin \left(45^\circ \right)=\frac{\sqrt{2}}{2},\cos \left(45^\circ \right)=\frac{\sqrt{2}}{2}\\[/latex], evaluate [latex]\tan \left(45^\circ \right)\\[/latex].
- Given [latex]\sin \left(\frac{5\pi }{6}\right)=\frac{1}{2},\text{cos}\left(\frac{5\pi }{6}\right)=-\frac{\sqrt{3}}{2},\text{evaluate}\sec \left(\frac{5\pi }{6}\right)\\[/latex].
Solution
Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.-
[latex]\begin{array}{l}\tan \left(45^\circ \right)=\frac{\sin \left(45^\circ \right)}{\cos \left(45^\circ \right)}\hfill \\ =\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}\hfill \\ =1\hfill \end{array}\\[/latex]
-
[latex]\begin{array}{l}\sec \left(\frac{5\pi }{6}\right)=\frac{1}{\cos \left(\frac{5\pi }{6}\right)}\hfill \\ =\frac{1}{-\frac{\sqrt{3}}{2}}\hfill \\ \begin{array}{l}=\frac{-2\sqrt{3}}{1}\hfill \\ =\frac{-2}{\sqrt{3}}\hfill \\ =-\frac{2\sqrt{3}}{3}\hfill \end{array}\hfill \end{array}\\[/latex]
Try It 5
Evaluate [latex]\text{csc}\left(\frac{7\pi }{6}\right)\\[/latex]. SolutionExample 6: Using Identities to Simplify Trigonometric Expressions
Simplify [latex]\frac{\sec t}{\tan t}\\[/latex].Solution
We can simplify this by rewriting both functions in terms of sine and cosine.[latex]\begin{array}\hfill \frac{\sec t}{\tan t}=\frac{\frac{1}{\cos t}}{\frac{\sin t}{\cos t}}\hfill& \text{To divide the functions, we multiply by the reciprocal.} \\=\frac{1}{\cos t}\frac{\cos t}{\sin t}\hfill&\text{Divide out the cosines.} \\ =\frac{1}{\sin t}\hfill&\text{Simplify and use the identity.}\\ =\csc t \end{array}\\[/latex]
By showing that [latex]\frac{\sec t}{\tan t}\\[/latex] can be simplified to [latex]\csc t[/latex], we have, in fact, established a new identity.[latex]\frac{\sec t}{\tan t}=\csc t\\[/latex]
Try It 6
Simplify [latex]\tan t\left(\cos t\right)\\[/latex]. SolutionAlternate Forms of the Pythagorean Identity
We can use these fundamental identities to derive alternative forms of the Pythagorean Identity, [latex]{\cos }^{2}t+{\sin }^{2}t=1\\[/latex]. One form is obtained by dividing both sides by [latex]{\cos }^{2}t:\\[/latex][latex]\begin{array}{c}\frac{{\cos }^{2}t}{{\cos }^{2}t}+\frac{{\sin }^{2}t}{{\cos }^{2}t}=\frac{1}{{\cos }^{2}t}\\ 1+{\tan }^{2}t={\sec }^{2}t\end{array}\\[/latex]
The other form is obtained by dividing both sides by [latex]{\sin }^{2}t:\\[/latex]
[latex]\begin{array}{c}\frac{{\cos }^{2}t}{{\sin }^{2}t}+\frac{{\sin }^{2}t}{{\sin }^{2}t}=\frac{1}{{\sin }^{2}t}\\ {\cot }^{2}t+1={\csc }^{2}t\end{array}\\[/latex]
A General Note: Alternate Forms of the Pythagorean Identity
[latex]1+{\tan }^{2}t={\sec }^{2}t\\[/latex]
[latex]{\cot }^{2}t+1={\csc }^{2}t\\[/latex]
Example 7: Using Identities to Relate Trigonometric Functions
If [latex]\text{cos}\left(t\right)=\frac{12}{13}\\[/latex] and [latex]t[/latex] is in quadrant IV, as shown in Figure 8, find the values of the other five trigonometric functions. Figure 8
Figure 8Solution
We can find the sine using the Pythagorean Identity, [latex]{\cos }^{2}t+{\sin }^{2}t=1[/latex], and the remaining functions by relating them to sine and cosine.[latex]\begin{array}{l}{\left(\frac{12}{13}\right)}^{2}+{\sin }^{2}t=1\hfill \\ \text{ }{\sin }^{2}t=1-{\left(\frac{12}{13}\right)}^{2}\hfill \\ \text{ }{\sin }^{2}t=1-\frac{144}{169}\hfill \\ \text{ }{\sin }^{2}t=\frac{25}{169}\hfill \\ \text{ }\sin t=\pm \sqrt{\frac{25}{169}}\hfill \\ \text{ }\sin t=\pm \frac{\sqrt{25}}{\sqrt{169}}\hfill \\ \text{ }\sin t=\pm \frac{5}{13}\hfill \end{array}\\[/latex]
The sign of the sine depends on the y-values in the quadrant where the angle is located. Since the angle is in quadrant IV, where the y-values are negative, its sine is negative, [latex]-\frac{5}{13}\\[/latex].
The remaining functions can be calculated using identities relating them to sine and cosine.
[latex]\begin{array}{l}\begin{array}{l}\begin{array}{l}\tan t=\frac{\sin t}{\cos t}=\frac{-\frac{5}{13}}{\frac{12}{13}}=-\frac{5}{12}\hfill \\ \begin{array}{l}\\ \sec t=\frac{1}{\cos t}=\frac{1}{\frac{12}{13}}=\frac{13}{12}\end{array}\hfill \end{array}\hfill \\ \csc t=\frac{1}{\sin t}=\frac{1}{-\frac{5}{13}}=-\frac{13}{5}\hfill \end{array}\\ \cot t=\frac{1}{\tan t}=\frac{1}{-\frac{5}{12}}=-\frac{12}{5}\end{array}\\[/latex]
Try It 7
If [latex]\sec \left(t\right)=-\frac{17}{8}[/latex] and [latex]0<t<\pi [/latex], find the values of the other five functions. SolutionA General Note: Period of a Function
The period [latex]P[/latex] of a repeating function [latex]f[/latex] is the number representing the interval such that [latex]f\left(x+P\right)=f\left(x\right)\\[/latex] for any value of [latex]x[/latex]. The period of the cosine, sine, secant, and cosecant functions is [latex]2\pi [/latex]. The period of the tangent and cotangent functions is [latex]\pi [/latex].Example 8: Finding the Values of Trigonometric Functions
Find the values of the six trigonometric functions of angle [latex]t[/latex] based on Figure 9. Figure 9
Figure 9Solution
[latex]\begin{array}{l}\sin t=y=-\frac{\sqrt{3}}{2}\\ \cos t=x=-\frac{1}{2}\\ \tan t=\frac{\sin t}{\cos t}=\frac{-\frac{\sqrt{3}}{2}}{-\frac{1}{2}}=\sqrt{3}\\ \sec t=\frac{1}{\cos t}=\frac{1}{-\frac{1}{2}}=-2\\ \csc t=\frac{1}{\sin t}=\frac{1}{-\frac{\sqrt{3}}{2}}=-\frac{2\sqrt{3}}{3}\\ \cot t=\frac{1}{\tan t}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\end{array}[/latex]
Try It 8
Find the values of the six trigonometric functions of angle [latex]t[/latex] based on Figure 10. Figure 10
Figure 10Example 9: Finding the Value of Trigonometric Functions
If [latex]\sin \left(t\right)=-\frac{\sqrt{3}}{2}[/latex] and [latex]\text{cos}\left(t\right)=\frac{1}{2}[/latex], find [latex]\text{sec}\left(t\right),\text{csc}\left(t\right),\text{tan}\left(t\right),\text{ cot}\left(t\right)[/latex].Solution
[latex]\begin{array}{l}\begin{array}{l}\\ \sec t=\frac{1}{\cos t}=\frac{1}{\frac{1}{2}}=2\end{array}\hfill \\ \csc t=\frac{1}{\sin t}=\frac{1}{-\frac{\sqrt{3}}{2}}-\frac{2\sqrt{3}}{3}\hfill \\ \tan t=\frac{\sin t}{\cos t}=\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}=-\sqrt{3}\hfill \\ \cot t=\frac{1}{\tan t}=\frac{1}{-\sqrt{3}}=-\frac{\sqrt{3}}{3}\hfill \end{array}[/latex]
Try It 9
If [latex]\sin \left(t\right)=\frac{\sqrt{2}}{2}[/latex] and [latex]\cos \left(t\right)=\frac{\sqrt{2}}{2}[/latex], find [latex]\text{sec}\left(t\right),\text{csc}\left(t\right),\text{tan}\left(t\right),\text{ and cot}\left(t\right)[/latex]. SolutionEvaluating Trigonometric Functions with a Calculator
We have learned how to evaluate the six trigonometric functions for the common first-quadrant angles and to use them as reference angles for angles in other quadrants. To evaluate trigonometric functions of other angles, we use a scientific or graphing calculator or computer software. If the calculator has a degree mode and a radian mode, confirm the correct mode is chosen before making a calculation. Evaluating a tangent function with a scientific calculator as opposed to a graphing calculator or computer algebra system is like evaluating a sine or cosine: Enter the value and press the TAN key. For the reciprocal functions, there may not be any dedicated keys that say CSC, SEC, or COT. In that case, the function must be evaluated as the reciprocal of a sine, cosine, or tangent. If we need to work with degrees and our calculator or software does not have a degree mode, we can enter the degrees multiplied by the conversion factor [latex]\frac{\pi }{180}\\[/latex] to convert the degrees to radians. To find the secant of [latex]30^\circ [/latex], we could press[latex]\text{(for a scientific calculator):}\frac{1}{30\times \frac{\pi }{180}}\text{COS}\\[/latex]
or
[latex]\text{(for a graphing calculator):}\frac{1}{\cos \left(\frac{30\pi }{180}\right)}\\[/latex]
How To: Given an angle measure in radians, use a scientific calculator to find the cosecant.
- If the calculator has degree mode and radian mode, set it to radian mode.
- Enter: [latex]1\text{ /}\\[/latex]
- Enter the value of the angle inside parentheses.
- Press the SIN key.
- Press the = key.
How To: Given an angle measure in radians, use a graphing utility/calculator to find the cosecant.
- If the graphing utility has degree mode and radian mode, set it to radian mode.
- Enter: [latex]1\text{ /}\\[/latex]
- Press the SIN key.
- Enter the value of the angle inside parentheses.
- Press the ENTER key.
Example 10: Evaluating the Secant Using Technology
Evaluate the cosecant of [latex]\frac{5\pi }{7}[/latex].Solution
For a scientific calculator, enter information as follows:[latex]\text{1 / ( 5 }\times \text{ }\pi \text{ / 7 ) SIN =}\\[/latex]
[latex]\csc \left(\frac{5\pi }{7}\right)\approx 1.279\\[/latex]
Try It 10
Evaluate the cotangent of [latex]-\frac{\pi }{8}\\[/latex]. SolutionKey Equations
| Tangent function | [latex]\tan t=\frac{\sin t}{\cos t}[/latex] |
| Secant function | [latex]\sec t=\frac{1}{\cos t}[/latex] |
| Cosecant function | [latex]\csc t=\frac{1}{\sin t}[/latex] |
| Cotangent function | [latex]\cot t=\frac{1}{\tan t}=\frac{\cos t}{\sin t}[/latex] |
Key Concepts
- The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle.
- The secant, cotangent, and cosecant are all reciprocals of other functions. The secant is the reciprocal of the cosine function, the cotangent is the reciprocal of the tangent function, and the cosecant is the reciprocal of the sine function.
- The six trigonometric functions can be found from a point on the unit circle.
- Trigonometric functions can also be found from an angle.
- Trigonometric functions of angles outside the first quadrant can be determined using reference angles.
- A function is said to be even if [latex]f\left(-x\right)=f\left(x\right)[/latex] and odd if [latex]f\left(-x\right)=-f\left(x\right)[/latex].
- Cosine and secant are even; sine, tangent, cosecant, and cotangent are odd.
- Even and odd properties can be used to evaluate trigonometric functions.
- The Pythagorean Identity makes it possible to find a cosine from a sine or a sine from a cosine.
- Identities can be used to evaluate trigonometric functions.
- Fundamental identities such as the Pythagorean Identity can be manipulated algebraically to produce new identities.
- The trigonometric functions repeat at regular intervals.
- The period [latex]P[/latex] of a repeating function [latex]f[/latex] is the smallest interval such that [latex]f\left(x+P\right)=f\left(x\right)[/latex] for any value of [latex]x[/latex].
- The values of trigonometric functions of special angles can be found by mathematical analysis.
- To evaluate trigonometric functions of other angles, we can use a calculator or computer software.
Glossary
- cosecant
- the reciprocal of the sine function: on the unit circle, [latex]\csc t=\frac{1}{y},y\ne 0[/latex]
- cotangent
- the reciprocal of the tangent function: on the unit circle, [latex]\cot t=\frac{x}{y},y\ne 0[/latex]
- identities
- statements that are true for all values of the input on which they are defined
- period
- the smallest interval [latex]P[/latex] of a repeating function [latex]f[/latex] such that [latex]f\left(x+P\right)=f\left(x\right)[/latex]
- secant
- the reciprocal of the cosine function: on the unit circle, [latex]\sec t=\frac{1}{x},x\ne 0[/latex]
- tangent
- the quotient of the sine and cosine: on the unit circle, [latex]\tan t=\frac{y}{x},x\ne 0[/latex]
Section Exercises
1. On an interval of [latex]\left[0,2\pi \right)[/latex], can the sine and cosine values of a radian measure ever be equal? If so, where? 2. What would you estimate the cosine of [latex]\pi [/latex] degrees to be? Explain your reasoning. 3. For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle? 4. Describe the secant function. 5. Tangent and cotangent have a period of [latex]\pi [/latex]. What does this tell us about the output of these functions? For the following exercises, find the exact value of each expression. 6. [latex]\tan \frac{\pi }{6}[/latex] 7. [latex]\sec \frac{\pi }{6}[/latex] 8. [latex]\csc \frac{\pi }{6}[/latex] 9. [latex]\cot \frac{\pi }{6}[/latex] 10. [latex]\tan \frac{\pi }{4}[/latex] 11. [latex]\sec \frac{\pi }{4}[/latex] 12. [latex]\csc \frac{\pi }{4}[/latex] 13. [latex]\cot \frac{\pi }{4}[/latex] 14. [latex]\tan \frac{\pi }{3}[/latex] 15. [latex]\sec \frac{\pi }{3}[/latex] 16. [latex]\csc \frac{\pi }{3}[/latex] 17. [latex]\cot \frac{\pi }{3}[/latex] For the following exercises, use reference angles to evaluate the expression. 18. [latex]\tan \frac{5\pi }{6}[/latex] 19. [latex]\sec \frac{7\pi }{6}[/latex] 20. [latex]\csc \frac{11\pi }{6}[/latex] 21. [latex]\cot \frac{13\pi }{6}[/latex] 22. [latex]\tan \frac{7\pi }{4}[/latex] 23. [latex]\sec \frac{3\pi }{4}[/latex] 24. [latex]\csc \frac{5\pi }{4}[/latex] 25. [latex]\cot \frac{11\pi }{4}[/latex] 26. [latex]\tan \frac{8\pi }{3}[/latex] 27. [latex]\sec \frac{4\pi }{3}[/latex] 28. [latex]\csc \frac{2\pi }{3}[/latex] 29. [latex]\cot \frac{5\pi }{3}[/latex] 30. [latex]\tan 225^\circ [/latex] 31. [latex]\sec 300^\circ [/latex] 32. [latex]\csc 150^\circ [/latex] 33. [latex]\cot 240^\circ [/latex] 34. [latex]\tan 330^\circ [/latex] 35. [latex]\sec 120^\circ [/latex] 36. [latex]\csc 210^\circ [/latex] 37. [latex]\cot 315^\circ [/latex] 38. If [latex]\text{sin}t=\frac{3}{4}[/latex], and [latex]t[/latex] is in quadrant II, find [latex]\cos t,\sec t,\csc t,\tan t,\cot t[/latex]. 39. If [latex]\text{cos}t=-\frac{1}{3}[/latex], and [latex]t[/latex] is in quadrant III, find [latex]\sin t,\sec t,\csc t,\tan t,\cot t[/latex]. 40. If [latex]\tan t=\frac{12}{5}[/latex], and [latex]0\le t<\frac{\pi }{2}[/latex], find [latex]\sin t,\cos t,\sec t,\csc t[/latex], and [latex]\cot t[/latex]. 41. If [latex]\sin t=\frac{\sqrt{3}}{2}[/latex] and [latex]\cos t=\frac{1}{2}[/latex], find [latex]\sec t,\csc t,\tan t[/latex], and [latex]\cot t[/latex]. 42. If [latex]\sin 40^\circ \approx 0.643\cos 40^\circ \approx 0.766\text{sec}40^\circ ,\text{csc}40^\circ ,\text{tan}40^\circ ,\text{and}\text{cot}40^\circ [/latex]. 43. If [latex]\text{sin}t=\frac{\sqrt{2}}{2}[/latex], what is the [latex]\text{sin}\left(-t\right)?[/latex] 44. If [latex]\text{cos}t=\frac{1}{2}[/latex], what is the [latex]\text{cos}\left(-t\right)?[/latex] 45. If [latex]\text{sec}t=3.1[/latex], what is the [latex]\text{sec}\left(-t\right)?[/latex] 46. If [latex]\text{csc}t=0.34[/latex], what is the [latex]\text{csc}\left(-t\right)?[/latex] 47. If [latex]\text{tan}t=-1.4[/latex], what is the [latex]\text{tan}\left(-t\right)?[/latex] 48. If [latex]\text{cot}t=9.23[/latex], what is the [latex]\text{cot}\left(-t\right)?[/latex] For the following exercises, use the angle in the unit circle to find the value of the each of the six trigonometric functions. 49. 50.
50.
 51.
51.
 For the following exercises, use a graphing calculator to evaluate.
52. [latex]\csc \frac{5\pi }{9}[/latex]
53. [latex]\cot \frac{4\pi }{7}[/latex]
54. [latex]\sec \frac{\pi }{10}[/latex]
55. [latex]\tan \frac{5\pi }{8}[/latex]
56. [latex]\sec \frac{3\pi }{4}[/latex]
57. [latex]\csc \frac{\pi }{4}[/latex]
58. [latex]\text{tan}98^\circ [/latex]
59. [latex]\cot 33^\circ [/latex]
60. [latex]\cot 140^\circ [/latex]
61. [latex]\sec 310^\circ [/latex]
For the following exercises, use identities to evaluate the expression.
62. If [latex]\tan \left(t\right)\approx 2.7[/latex], and [latex]\sin \left(t\right)\approx 0.94[/latex], find [latex]\cos \left(t\right)[/latex].
63. If [latex]\tan \left(t\right)\approx 1.3[/latex], and [latex]\cos \left(t\right)\approx 0.61[/latex], find [latex]\sin \left(t\right)[/latex].
64. If [latex]\csc \left(t\right)\approx 3.2[/latex], and [latex]\cos \left(t\right)\approx 0.95[/latex], find [latex]\tan \left(t\right)[/latex].
65. If [latex]\cot \left(t\right)\approx 0.58[/latex], and [latex]\cos \left(t\right)\approx 0.5[/latex], find [latex]\csc \left(t\right)[/latex].
66. Determine whether the function [latex]f\left(x\right)=2\sin x\cos x[/latex] is even, odd, or neither.
67. Determine whether the function [latex]f\left(x\right)=3{\sin }^{2}x\cos x+\sec x[/latex] is even, odd, or neither.
68. Determine whether the function [latex]f\left(x\right)=\sin x - 2{\cos }^{2}x[/latex] is even, odd, or neither.
69. Determine whether the function [latex]f\left(x\right)={\csc }^{2}x+\sec x[/latex] is even, odd, or neither.
For the following exercises, use identities to simplify the expression.
70. [latex]\csc t\tan t[/latex]
71. [latex]\frac{\sec t}{\csc t}[/latex]
72. The amount of sunlight in a certain city can be modeled by the function [latex]h=15\cos \left(\frac{1}{600}d\right)[/latex], where [latex]h[/latex] represents the hours of sunlight, and [latex]d[/latex] is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42nd day of the year. State the period of the function.
73. The amount of sunlight in a certain city can be modeled by the function [latex]h=16\cos \left(\frac{1}{500}d\right)[/latex], where [latex]h[/latex] represents the hours of sunlight, and [latex]d[/latex] is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267th day of the year. State the period of the function.
74. The equation [latex]P=20\sin \left(2\pi t\right)+100[/latex] models the blood pressure, [latex]P[/latex], where [latex]t[/latex] represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?
75. The height of a piston, [latex]h[/latex], in inches, can be modeled by the equation [latex]y=2\cos x+6[/latex], where [latex]x[/latex] represents the crank angle. Find the height of the piston when the crank angle is [latex]55^\circ [/latex].
76. The height of a piston, [latex]h[/latex], in inches, can be modeled by the equation [latex]y=2\cos x+5[/latex], where [latex]x[/latex] represents the crank angle. Find the height of the piston when the crank angle is [latex]55^\circ [/latex].
For the following exercises, use a graphing calculator to evaluate.
52. [latex]\csc \frac{5\pi }{9}[/latex]
53. [latex]\cot \frac{4\pi }{7}[/latex]
54. [latex]\sec \frac{\pi }{10}[/latex]
55. [latex]\tan \frac{5\pi }{8}[/latex]
56. [latex]\sec \frac{3\pi }{4}[/latex]
57. [latex]\csc \frac{\pi }{4}[/latex]
58. [latex]\text{tan}98^\circ [/latex]
59. [latex]\cot 33^\circ [/latex]
60. [latex]\cot 140^\circ [/latex]
61. [latex]\sec 310^\circ [/latex]
For the following exercises, use identities to evaluate the expression.
62. If [latex]\tan \left(t\right)\approx 2.7[/latex], and [latex]\sin \left(t\right)\approx 0.94[/latex], find [latex]\cos \left(t\right)[/latex].
63. If [latex]\tan \left(t\right)\approx 1.3[/latex], and [latex]\cos \left(t\right)\approx 0.61[/latex], find [latex]\sin \left(t\right)[/latex].
64. If [latex]\csc \left(t\right)\approx 3.2[/latex], and [latex]\cos \left(t\right)\approx 0.95[/latex], find [latex]\tan \left(t\right)[/latex].
65. If [latex]\cot \left(t\right)\approx 0.58[/latex], and [latex]\cos \left(t\right)\approx 0.5[/latex], find [latex]\csc \left(t\right)[/latex].
66. Determine whether the function [latex]f\left(x\right)=2\sin x\cos x[/latex] is even, odd, or neither.
67. Determine whether the function [latex]f\left(x\right)=3{\sin }^{2}x\cos x+\sec x[/latex] is even, odd, or neither.
68. Determine whether the function [latex]f\left(x\right)=\sin x - 2{\cos }^{2}x[/latex] is even, odd, or neither.
69. Determine whether the function [latex]f\left(x\right)={\csc }^{2}x+\sec x[/latex] is even, odd, or neither.
For the following exercises, use identities to simplify the expression.
70. [latex]\csc t\tan t[/latex]
71. [latex]\frac{\sec t}{\csc t}[/latex]
72. The amount of sunlight in a certain city can be modeled by the function [latex]h=15\cos \left(\frac{1}{600}d\right)[/latex], where [latex]h[/latex] represents the hours of sunlight, and [latex]d[/latex] is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42nd day of the year. State the period of the function.
73. The amount of sunlight in a certain city can be modeled by the function [latex]h=16\cos \left(\frac{1}{500}d\right)[/latex], where [latex]h[/latex] represents the hours of sunlight, and [latex]d[/latex] is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267th day of the year. State the period of the function.
74. The equation [latex]P=20\sin \left(2\pi t\right)+100[/latex] models the blood pressure, [latex]P[/latex], where [latex]t[/latex] represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?
75. The height of a piston, [latex]h[/latex], in inches, can be modeled by the equation [latex]y=2\cos x+6[/latex], where [latex]x[/latex] represents the crank angle. Find the height of the piston when the crank angle is [latex]55^\circ [/latex].
76. The height of a piston, [latex]h[/latex], in inches, can be modeled by the equation [latex]y=2\cos x+5[/latex], where [latex]x[/latex] represents the crank angle. Find the height of the piston when the crank angle is [latex]55^\circ [/latex].
Licenses & Attributions
CC licensed content, Shared previously
- Even and Odd Trigonometric Identities. Authored by: Mathispower4u. License: All Rights Reserved. License terms: Standard YouTube License.
- The Reciprocal, Quotient, and Pythagorean Identities . Authored by: Mathispower4u. License: All Rights Reserved. License terms: Standard YouTube License.
- Determining Trigonometric Function Values on the Calculator . Authored by: Mathispower4u. License: All Rights Reserved.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
